Proving the results for the trace of a matrix

[PainterGuy]

Homework Statement

Verifying the trace problem.

Relevant Equations

Please check my work.

Hi,

I was trying to do the following problem. I was able to do the part in pink highlight (please check "My attempt") but the part in orange highlight makes no sense to me. I'd really appreciate if you could help me to solve the part in orange. Thank you!

My attempt:

The solution presented below doesn't make much sense to me either.

I do not understand the writing for step in green highlight below. I interpret it as shown below. Please correct me if I'm wrong.

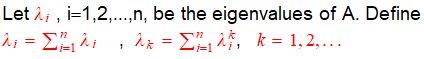
Also I do not understand the reason for using Newton's identity and how it works in this case.

 

[andrewkirk]

What theorem are you trying to prove?

It looks to me as though all of the pink and blue bits are definitions rather than theorems, except for the last line of the pink part and the second equality in each line of the pink part.
Since the second equality in each pink row follows easily from the first equality (the "definition" part of the row), we are left with the last row of the pink part as the theorem you have to prove.
If so, why have you coloured that last row pink, if pink indicates the parts you have managed to prove?

What do you mean by "the orange part makes no sense to me"? It just gives definitions for the scalars $\alpha_1, ..., \alpha_n$. For it to make sense, all you need is to understand the meaning of the RHS of each of those equalities, which I infer from your post above that you already do.

I have not worked through the above in detail, and have not seen Newton's identity before, but I can correct your interpretation of the green bit. The LHS is a capital Lambda, and RHS entries are lower case lambdas. So the the equation is:
$$\Lambda_k = \sum_{i=1}^n \lambda_i{}^k,\quad\quad\quad\quad k\in\mathbb N$$
This is another definition, defining $\Lambda_k$, which differs from $\lambda_k$.

 

[PainterGuy]

It looks to me as though all of the pink and blue bits are definitions rather than theorems

Thank you but which ones are the blue bits? I don't think there are any blue bits. Could you please clarify?

 

[andrewkirk]

Sorry I meant orange rather than blue. I sometimes get my colours mixed up!

 

[PainterGuy]

I still cannot understand how the Newton's identity is formed using 'Λ' and 'α', and how come it equates to zero? Could you please help?

$$\Lambda _{k}+\alpha _{1}\Lambda _{k-1}+...+\alpha _{k-1}\Lambda _{1}+k\alpha _{k}=0$$
for k=1,2,...,n

PS:
Helpful link: https://en.wikipedia.org/wiki/Newton's_identities#Application_to_the_characteristic_polynomial_of_a_matrix