Pulley Free Body Diagram Problem

[MG5]

In the figure below, m1 = 10.5 kg and m2 = 3.5 kg. The coefficient of static friction between m1 and the horizontal surface is 0.50, and the coefficient of kinetic friction is 0.30.

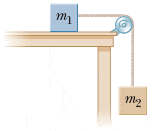
I've drawn the free body diagram myself and labeled it but don't know how to structure the equations and stuff.

And I forgot to add what the two questions were.

a.) If the system is released from rest, what will its acceleration be?b.) If the system is set in motion with m2 moving downward, what will be the acceleration of the system?

 

[Simon Bridge]

Take each mass separately, and write $\sum F = ma$ for each one.

1. pick a direction for positive - "down" is good for m2 and "to the right" for m1.
2. write down the forces in a row with plus signs between them - some of the forces will be negative.
3. put an = sign after the forces
4. put "ma" after the = sign.

Repeat for the other mass. (make sure you use the right m's)
Since the cord does nt stretch or compress, the acceleration of m1 is the same as the acceleration of m2 so you can give them the same symbol a.

So for m2 you have m₂g-T=m₂a
Now you do it for mass m1.

 

[MG5]

Take each mass separately, and write $\sum F = ma$ for each one.

1. pick a direction for positive - "down" is good for m2 and "to the right" for m1.
2. write down the forces in a row with plus signs between them - some of the forces will be negative.
3. put an = sign after the forces
4. put "ma" after the = sign.

Repeat for the other mass. (make sure you use the right m's)
Since the cord does nt stretch or compress, the acceleration of m1 is the same as the acceleration of m2 so you can give them the same symbol a.

So for m2 you have m₂g-T=m₂a
Now you do it for mass m1.

Ok, makes sense. So wouldn't m1 be just T=m1a

and then substitute that into m2g-T=m2a so it would become m2g-m1a=m2a

That right?

 

[Simon Bridge]

That's the one ... now check it makes sense: you have T the same for both diagrams and a the same for both.

Now you have two equations and two unknowns.
Have you solved simultaneous equations before?
[edit] you are ahead of me ;)

Now you just need to rearrange the equation to make it look like a=<some stuff> and you are done.

 

[MG5]

That's the one ... now check it makes sense: you have T the same for both diagrams and a the same for both.

Now you have two equations and two unknowns.
Have you solved simultaneous equations before?
[edit] you are ahead of me ;)

Now you just need to rearrange the equation to make it look like a=<some stuff> and you are done.

a= m2g-m1a / m2

I guess? doesn't look right though.

 

[Simon Bridge]

You still have an "a" on the RHS. Put all the a's on the LHS.

It's called "solving for a" or "making a the subject".

 

[MG5]

You still have an "a" on the RHS. Put all the a's on the LHS.

It's called "solving for a" or "making a the subject".

I knew something wasnt right. Didnt even notice it though.

How about a=(m2/m1+m2)g

 

[Simon Bridge]

Here's how to check your answers:
$$a=\frac{m_2}{m_1+m_2}g$$
... see how the fraction is basically mass-divided-by-mass (so you have units of acceleration on both sides - always a good sign) and it comes out less than 1? This means the acceleration of the blocks will be less than the acceleration due to gravity. Which is what you'd expect - so you can feel good about it.

 

[MG5]

Here's how to check your answers:
$$a=\frac{m_2}{m_1+m_2}g$$
... see how the fraction is basically mass-divided-by-mass (so you have units of acceleration on both sides - always a good sign) and it comes out less than 1? This means the acceleration of the blocks will be less than the acceleration due to gravity. Which is what you'd expect - so you can feel good about it.

ok. from there would it be taken even further to a=1/3g

And I still don't understand how I'd find the acceleration from this. do i eventually use f=ma

 

[Simon Bridge]

You usually have values for the masses ... so if m1=1kg and m2=4kg then a = 0.8g is your acceleration. Anyone riding on m2 would feel lighter.

If you are not given values then "find the acceleration" means "find the equation that would get you the acceleration if only you had the other values..."

If the table had friction - which they tend to do - the friction force would act on m1 and resist the motion in proportion with the weight ... so friction = $f = \mu m_1g$ ... how does that change your calculation?

 

[MG5]

You usually have values for the masses ... so if m1=1kg and m2=4kg then a = 0.8g is your acceleration. Anyone riding on m2 would feel lighter.

If you are not given values then "find the acceleration" means "find the equation that would get you the acceleration if only you had the other values..."

If the table had friction - which they tend to do - the friction force would act on m1 and resist the motion in proportion with the weight ... so friction = $f = \mu m_1g$ ... how does that change your calculation?

I do have values for the masses. 10.5 and 3.5. and that last equation you put i don't even know what that means. haven't gotten to that in class yet. and yeah there's friction too. 0.50 of static and 0.30 kinetic

 

[Simon Bridge]

The friction is important - it adds another force in with the free-body diagrams.
The calculation you did assumes the table has no friction.

For the friction, you write $\mu_s=0.50$ for static and $\mu_k=0.30$ for kinetic.
Coefficients of friction have no units ... the friction force always opposes motion, and it is equal to the coefficient times how hard the object is pressing against the surface - called the "normal force" for being at right-angles to the surface.

To use the masses, you'd need to know which is which ... and the units - never leave the units off.

So, anyway - now you need to go back to the free-body diagrams and work out which one has friction and what kind, put an extra arrow into show the friction force and it's direction. This gives you an extra force to write in on step 2 in post #2. Good practice ;)

 

[PhanthomJay]

We seem to have lost track of the original problem and questions. Both require knowledge of the concepts of static and kinetic friction forces. If you are not yet familiar with the calculation for friction forces, wait until you study about it before trying this problem.

 

[Simon Bridge]

Not lost track - no - just did the frictionless case as an exercise first ;)
But you are correct - I was kinda thinking that this was assigned work ... only later it transpires that the class has not covered friction yet.

It's the next logical extension for free-body diagrams.
Perhaps practice some frictionless problems to get used to the routine?

 

[MG5]

We seem to have lost track of the original problem and questions. Both require knowledge of the concepts of static and kinetic friction forces. If you are not yet familiar with the calculation for friction forces, wait until you study about it before trying this problem.

Yeah we haven't gone over it yet but we do today in class. But if we complete the assignment before class starts we get 10% extra credit so that's why I was trying to do it. But its not actually due till midnight tonight.

 

[MG5]

I found part b to this. Its .245 m/s squared. But still can't find a.

Found part a too. Its just 0