shivajikobardan
- 637
- 54
Please review my proof. Is this correct or not?

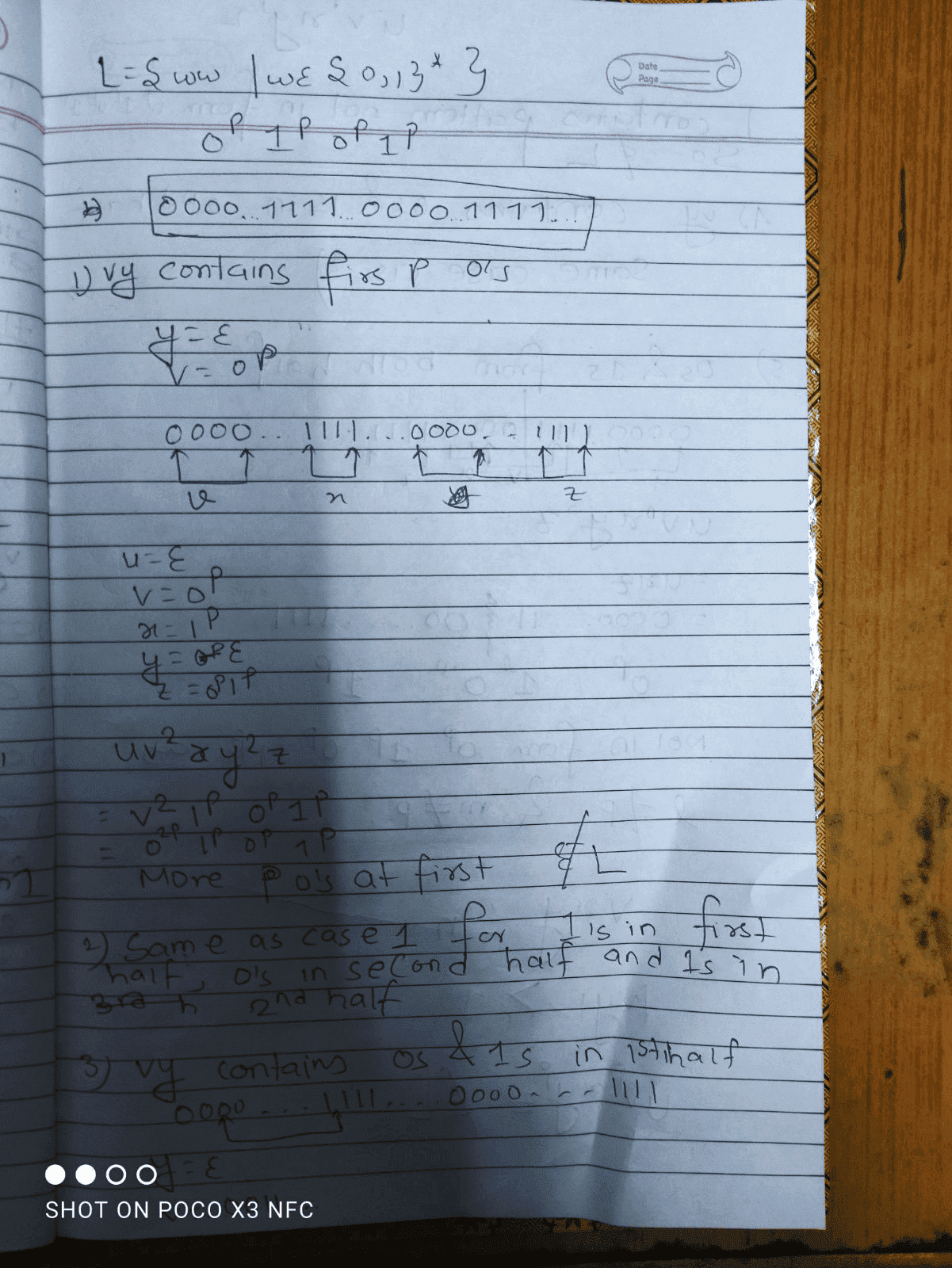
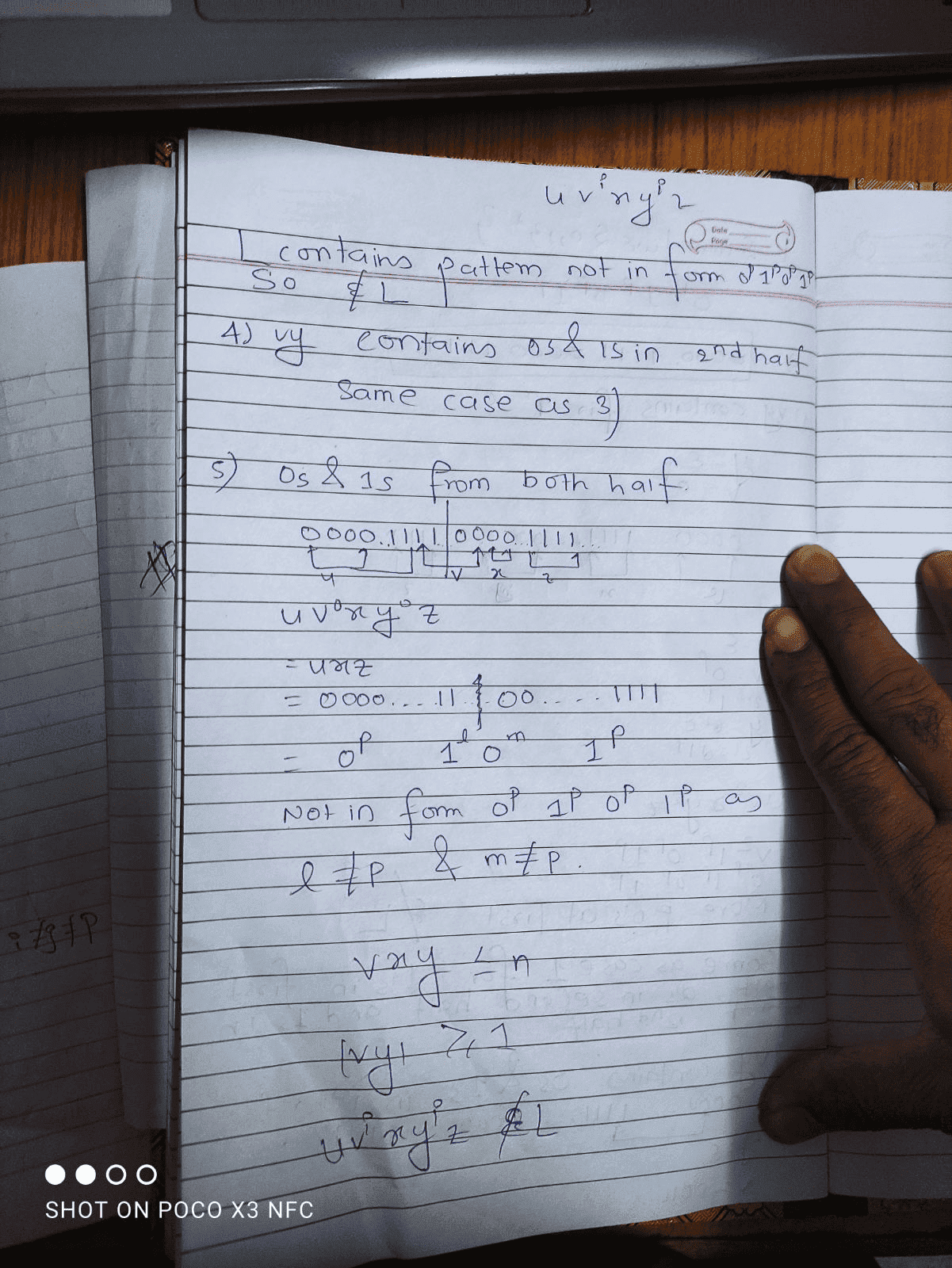
The forum discussion centers on the proof of the Pumping Lemma for the language L = 0^p 1^p 0^p 1^p. The original proof is critiqued for ambiguities and violations of the lemma's conditions, particularly in cases where the segments of the string are defined. Specific issues include the handling of cases where v = 0^p and y = ε, as well as the clarity of case descriptions. The discussion emphasizes the need for a more structured and detailed proof, including explicit definitions and clear case analysis.
PREREQUISITESStudents of theoretical computer science, mathematicians focusing on formal languages, and anyone involved in writing or analyzing mathematical proofs will benefit from this discussion.