mistymoon_38
- 18
- 0
[SOLVED] Puzzle with Vectors--almost there!
The sum of three vectors is zero. The magnitude of the first vector is twice the magnitude of the second. The first and second vectors are perpendicular. The direction of the third vector is along the negative x-axis. What are the directions of the other two vectors? There are two possible sets of answers. For both sets of answers, give the directions in standard polar form
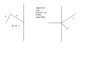
To make two perpendicular vectors with one twice the length of the other:
Set up a right triangle with side lengths 1 and 2 and therefore hypontenuse=root of 5
Because the third vector(hypontenuse) is along the negative x direction, the triangle is placed on a coordinate system with the hypotenuse like that. However, so the sum of all three is 0, vector 1 must be projected over the y-axis, and vector 2 over the y and x-axis. So they all cancel out, because vector 3 can be any negative value, root 5 was just used to determine the angles of the other vectors
Therefore, the angle of the first vector is 180-arcsin(1/root5)=26.6 degrees and the second is 360-(180-90-(180-26.6)=296.6 degrees
Assuming this is all correct, I still have no clue what the second possible set of answers would be. Any insights?
Homework Statement
The sum of three vectors is zero. The magnitude of the first vector is twice the magnitude of the second. The first and second vectors are perpendicular. The direction of the third vector is along the negative x-axis. What are the directions of the other two vectors? There are two possible sets of answers. For both sets of answers, give the directions in standard polar form
Homework Equations
The Attempt at a Solution
To make two perpendicular vectors with one twice the length of the other:
Set up a right triangle with side lengths 1 and 2 and therefore hypontenuse=root of 5
Because the third vector(hypontenuse) is along the negative x direction, the triangle is placed on a coordinate system with the hypotenuse like that. However, so the sum of all three is 0, vector 1 must be projected over the y-axis, and vector 2 over the y and x-axis. So they all cancel out, because vector 3 can be any negative value, root 5 was just used to determine the angles of the other vectors
Therefore, the angle of the first vector is 180-arcsin(1/root5)=26.6 degrees and the second is 360-(180-90-(180-26.6)=296.6 degrees
Assuming this is all correct, I still have no clue what the second possible set of answers would be. Any insights?