Puzzled about the non-teaching of Monte Carlo method(s) for error analysis

[hutchphd]

Mostly I was talking about process control and medical statistical sampling applications.
Clearly techniques developed by von Neumann, Fermi, and Ulam will not be trivial, but they were using the techniques for simulations otherwise not doable (at least with their contemporary computing resources). Again they are certainly useful where they are useful.

 

[fluidistic]

I appreciate your exchanges, people.
Going back to the resistor measurement. Imagine I want to measure a resistor's resistance, and that it's true value is 308 ohm. I use a current source giving a current of intensity 25 uA (uncertainty or standard deviation of 10%) and I measure a voltage of 7.7 mV (SD 2% as in hutchphd's example). A lucky strike, I know, this yields the true value for R, but this doesn't matter.

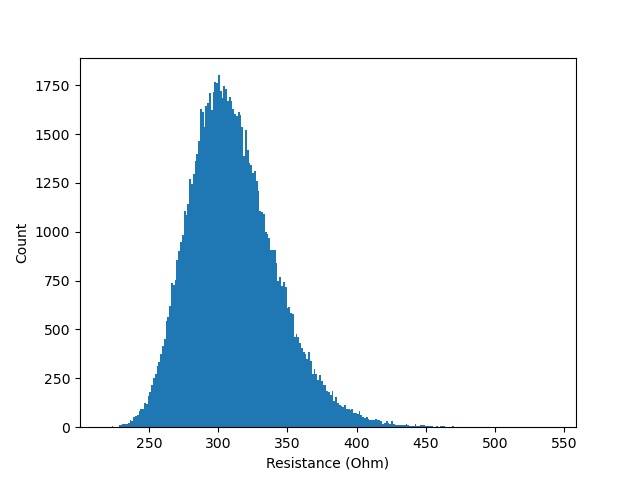
Out of a single measurement, Monte Carlo gives me the following histogram for R:

The obtained simulations give me that R = 308 +16 -14 ohm. I reported the median and the 68% confidence interval, but of course I can get the mean, standard deviation and any other commonly reported stats. The analytical formula tells me that R = 308 +/- 32 Ohm (it makes sense, it's slightly higher than 10% of R, which it should since the biggest uncertainty comes from the current, which is 10%). I am not sure why there is such a disparity between MC and the analytical formula, as the histogram does not differ that much from a Gaussian. I probably goofed with the confidence interval.

Anyway, if I am not doing things the wrong way, a sensitivity analysis tells me what we already knew, i.e. that the histogram will not change much even if the standard deviation of the voltage reaches 0 (for example by repeating the voltage measurement reading an infinite number of times). But it also shows the histogram of R I would get if I managed to reduce the uncertainty in the current by a factor 10 (by making 100 measurements of the current, assuming that a lot of sources of error introduced by the use of an ammeter are negligible, which is not a given in real life conditions). See it for yourself:

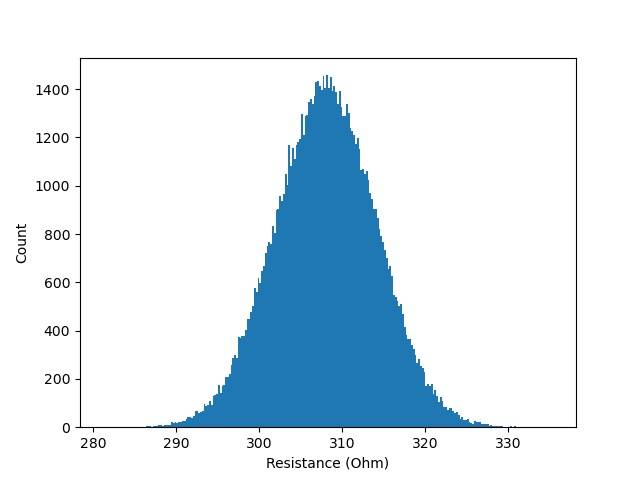
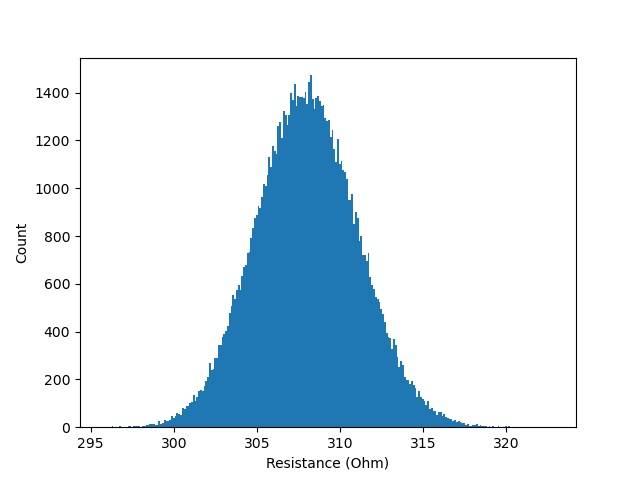
With MC, I have to input the probability distributions of I and V, and it turns out that if I repeat the experiment N times, the uncertainty in either I or V will decrease by a factor of sqrt(N). This is not a property of the analytical formula alone, it's just a fact about the standard deviation of the mean, I believe. So I can use this factor and repeat the sensitivity analysis by reducing the standard deviation of I and/or V as I like. In this way, I do not quite entirely see why MC gives inferior insight than the analytical formula. The more I think about it, the more I get immersed in the complexity. For example, I would never do, in real life, the 4 measurements of I and 100 measurements of V. It is not as simple as that. If, for an experiment, only V is measured and in the other experiment only I is measured, then it's probably not exactly the same setup, I am not sure if it is as easy to analyze the results from such experiments. Here in my example of a resistor of 308 ohm, it may not matter, but if the resistance was about 1 ohm, plugging an ammeter could be quite annoying and change drastically the result.

I actually enjoy this example, because it could be a real life good example, since measuring accurately a resistance is sometimes required.

 

[hutchphd]

Out of a single measurement, Monte Carlo gives me the following histogram for R:

The obtained simulations give me that R = 308 +16 -14 ohm.

.

I do not understand quoted simulation passband and this graph. They are clearly inconsistent. The width on the graph is clearly 60 ohms or more. Am I not understanding?

 

[fluidistic]

.

I do not understand quoted simulation passband and this graph. They are clearly inconsistent. The width on the graph is clearly 60 ohms or more. Am I not understanding?

Yeah, like I said I probably goofed in the reported percentiles. I will check my code tomorrow.

 

[fluidistic]

It turns out I didn't make any mistake there (I think!). It may seem counter intuitive, so here is the same plot (well another such simulation) with the mean, 68.27 interval, 95.45 and 99.73 intervals (1, 2 and 3 SD for a Gaussian). It may be an artifact of the histogram, which contains "only" 250 bins, so beware.

There are 100,000 values of R.
Lower bound 3 sigma comes at number 270. (as it should, this is 2.7%, or 1-0.9973). The value of R is 239 ohm.
Lower bound 2 sigma comes at number 4,650. (again, trivially as it should). R = 263 ohm.
Lower bound 1 sigma comes at number 31,730. (idem, ad nauseam) R = 294 ohm.
Mean comes at roughly number 50,000. (do I even need to think anymore at this point?) R = 308 ohm.
Upper bound 1 sigma comes at number 68,270. R = 324 ohm.
Upper bound 2 sigma comes at number 95,450. R = 372 ohm.
Upper bound 3 sigma comes at number 99,730. R = 430 ohm.

If this holds, this also means that even in this simple case where the histogram looked somewhat similar to a Gaussian at very frst glance (sure, it's visibly not a Gaussian, but it doesn't look that different at first glance), the common analytical formula overestimates significantly the uncertainty, assuming MC is more accurate

 

[FactChecker]

Since R is always positive, it was a given that the distribution is not Gaussian. There are some common distributions that are always positive. The log-normal distribution might be a good fit with the correct parameters. It would be interesting to calculate the mean and variance of the associated ln(R) values and see if the log-normal distribution with those parameters is a good fit. (see https://en.wikipedia.org/wiki/Log-normal_distribution#Generation_and_parameters)

 

[hutchphd]

It turns out I didn't make any mistake there (I think!). It may seem counter intuitive, so here is the same plot (well another such simulation) with the mean, 68.27 interval, 95.45 and 99.73 intervals (1, 2 and 3 SD for a Gaussian). It may be an artifact of the histogram, which contains "only" 250 bins, so beware.

There is no way 68% of the curve area is between the orange lines.
What is a count??
Of course I have no way to check this as previously discussed.
The one SD number will be ~10% of the average=30ohms. You have done something wrong.
For a Guassian FWHM (Full width half max) is 2.3 sigma

 

[hutchphd]

Since R is always positive, it was a given that the distribution is not Gaussian.

Of course that is true. But for things within one SD it will be a very good approximation. The "wings" will be less so. But unless I misunderstand this calculation is nonsense.

 

[Vanadium 50]

There is no way 68% of the curve area is between the orange lines.

I agree. The first blue plot has a FWHM of around 75-80Ω, which means a standard deviation around 32-34Ω, which is 10-11%. That agrees with what was put in.

+16 -14 ohm cannot possibly be right. If your worst measurement is 10%, you can't get a 5% measurement by combining it with other uncertainties. It doesn't match the plot.

Somehow this is evidence that the analytic formula is wrong? I would say instead that it's evidence that an over-reliance on MC makes it harder to spot even obvious errors.

 

[FactChecker]

I would say instead that it's evidence that an over-reliance on MC makes it harder to spot even obvious errors.

Overconfidence is probably a better word than over-reliance (although the OP is actually questioning the results). Results should be critically examined, whether they are from classical analysis or from MC simulations. In fact, this resistance example is as simple as you will ever see. (I think that the problem statement that current and voltage are assumed to be uncorrelated might invalidate any approach.) When the subjects become network theory, resource allocation, spares positioning, queueing theory, random walk, etc., even simple problems are difficult analytically. In those, the slightest complication can make analytical approaches unreasonable.
I am not saying that one should not thoroughly understand the statistical analysis methods. I am just saying that Monte Carlo simulations are the only practical way to address a great many problems. I believe that the OP implied that the analytical theory should be de-emphasized. I disagree with that. I also disagree with comments implying that Monte Carlo methods are just an easy and sloppy substitute for good analysis. MC methods are an essential addition to the toolset.

 

[Vanadium 50]

Overconfidence is probably a better word than over-reliance

That's fair.

I am not saying that one should not thoroughly understand the statistical analysis methods. I am just saying that Monte Carlo simulations are the only practical way to address a great many problems

I agree with that (example to follow). I don't think anyone is arguing against that.

I believe that the OP implied that the analytical theory should be de-emphasized.

That's what people are arguing against.

I have no objection to MC methods. Use 'em myself. But it's a case of the right tool for the right job.

Promised example: I have a copper bus bar of dimensions (l,w,h) and with (possibly different) uncertainties on each dimension. However, the total uncertainty on the volume is much less than any of those uncertainties. (Perhaps it was very accurately weighed). What is the uncertainty on its resistance?

While I think I could solve it analytically (but only because the cross-sectional shape factors out), it's probably simpler to run an MC.

 

[fluidistic]

I am sorry, I am destroyedly tired. I also want to understand what's wrong with the data or histogram.
Python code that generates a plot like I've provided:

import random as rdn
import statistics as sts
import matplotlib.pyplot as plt
import numpy as np

def one_run():
    I = rdn.gauss(0.025e-3, 0.1*0.025e-3)
    V = rdn.gauss(77e-4, 0.02*77e-4)
    R = V/I
    return R

resistances = []
for run in range(100000):
    result = one_run()
    resistances.append(result)

the_median = sts.median(resistances)
the_mean = sts.mean(resistances)
lower_confidence = np.percentile(resistances, 100-68.3)
upper_confidence = np.percentile(resistances, 68.3)
lower_2SD = np.percentile(resistances, 4.65)
lower_3SD = np.percentile(resistances, 0.27)
upper_2SD = np.percentile(resistances, 95.45)
upper_3SD = np.percentile(resistances, 99.73)

print('median', the_median)
print('mean', the_mean)
print('minus window', the_median - lower_confidence)
print('upper window', upper_confidence - the_median)
#print(resistances)
fig, ax = plt.subplots(1, 1)

ax.hist(resistances, bins=250)
plt.axvline(lower_2SD, color='yellow')
plt.axvline(upper_2SD, color='yellow')
plt.axvline(lower_3SD, color='green')
plt.axvline(upper_3SD, color='green')
plt.axvline(the_median, color='red')
plt.axvline(lower_confidence, color='orange')
plt.axvline(upper_confidence, color='orange')

ax.set_xlabel('Resistance (ohm)')
ax.set_ylabel('Count')
#plt.show()
plt.savefig('R_hist.jpg')
plt.close()

Of course, I do not ask for a debug, but if you want to check it out yourself, feel free to use the code. I will debug when I can, as I would like to understand what is going on.

Edit: I figured out the mistake, sorry. (Facepalm, shameful face). I will correct it. The histogram is correct I think. But not the error bars, as you have pointed out.

 

[fluidistic]

I am sorry, I am destroyedly tired. I also want to understand what's wrong with the data or histogram.
Python code that generates a plot like I've provided:

import random as rdn
import statistics as sts
import matplotlib.pyplot as plt
import numpy as np

def one_run():
    I = rdn.gauss(0.025e-3, 0.1*0.025e-3)
    V = rdn.gauss(77e-4, 0.02*77e-4)
    R = V/I
    return R

resistances = []
for run in range(100000):
    result = one_run()
    resistances.append(result)

the_median = sts.median(resistances)
the_mean = sts.mean(resistances)
lower_confidence = np.percentile(resistances, 100-68.3)
upper_confidence = np.percentile(resistances, 68.3)
lower_2SD = np.percentile(resistances, 4.65)
lower_3SD = np.percentile(resistances, 0.27)
upper_2SD = np.percentile(resistances, 95.45)
upper_3SD = np.percentile(resistances, 99.73)

print('median', the_median)
print('mean', the_mean)
print('minus window', the_median - lower_confidence)
print('upper window', upper_confidence - the_median)
#print(resistances)
fig, ax = plt.subplots(1, 1)

ax.hist(resistances, bins=250)
plt.axvline(lower_2SD, color='yellow')
plt.axvline(upper_2SD, color='yellow')
plt.axvline(lower_3SD, color='green')
plt.axvline(upper_3SD, color='green')
plt.axvline(the_median, color='red')
plt.axvline(lower_confidence, color='orange')
plt.axvline(upper_confidence, color='orange')

ax.set_xlabel('Resistance (ohm)')
ax.set_ylabel('Count')
#plt.show()
plt.savefig('R_hist.jpg')
plt.close()

Of course, I do not ask for a debug, but if you want to check it out yourself, feel free to use the code. I will debug when I can, as I would like to understand what is going on.

Edit: I figured out the mistake, sorry. (Facepalm, shameful face). I will correct it. The histogram is correct I think. But not the error bars, as you have pointed out.

Tadum:
Uncertainties that doesn't vary much from the Gaussian (which makes sense, assuming the histogram has no hidden surprises).
minus window 28.76204359267797
upper window 34.91842045829611
Updated plot

 

[hutchphd]

This seems a perfect cautionary tale to me. .

 

[Vanadium 50]

minus window 28.76204359267797
upper window 34.91842045829611

If you can't be accurate, at least be precise...

 

[FactChecker]

This seems a perfect cautionary tale to me.

It looks like the Monte Carlo simulation was only a couple of simple lines of code that were always correct. It was the data post-analysis that went wrong. The real cautionary tale might about a broader issue: The assumed zero correlation of the voltage and current through a (fixed?) resistance. That is something to be concerned about no matter what approach is taken. IMHO, there can be less emphasis on difficult theoretical analysis and more on frequent, fundamental, issues like whether variables are correlated, self-selecting samples, and other sources of bias that are so often overlooked.

 

[fluidistic]

It looks like the Monte Carlo simulation was only a couple of simple lines of code that were always correct. It was the data post-analysis that went wrong. The real cautionary tale might about a broader issue: The assumed zero correlation of the voltage and current through a (fixed?) resistance. That is something to be concerned about no matter what approach is taken. IMHO, there can be less emphasis on difficult theoretical analysis and more on frequent, fundamental, issues like whether variables are correlated, self-selecting samples, and other sources of bias that are so often overlooked.

Sure, one must be cautious. Also, although I have performed a simple sensitivity test, which showed the effect of improving the accuracy of either I or V and concluded like the analytical formula, I haven't obtained numbers but just histograms. I should investigate how I could objectively determine the improvements.
About the non correlation between I and V, do you mean that in the real world, R is a function of temperature and that using a current creates a Joule effect that affects T, thus R and thus V? Or do you have something else in mind?

 

[FactChecker]

About the non correlation between I and V, do you mean that in the real world, R is a function of temperature and that using a current creates a Joule effect that affects T, thus R and thus V? Or do you have something else in mind?

Sorry. I may have missed some explanation. It is not clear to me what the experiment is. If a power supply is placing a voltage across a single resistor with constant resistance, the voltage and current are definitely correlated. You are simulating uncorrelated voltage and current. Are you talking about measurements with uncorrelated measurement errors? Are you talking about real voltage errors in the power supply? Both? Something else? I am confused.

 

[fluidistic]

Sorry. I may have missed some explanation. It is not clear to me what the experiment is. If a power supply is placing a voltage across a single resistor with constant resistance, the voltage and current are definitely correlated. You are simulating uncorrelated voltage and current. Are you talking about measurements with uncorrelated measurement errors? Are you talking about real voltage errors in the power supply? Both? Something else? I am confused.

There's no real experiment, so it's up to us. I mentioned a current source (not a voltage source), but we're not forced to focus on this. I am just wondering the sources of correlations between I and V in a real life experiment.
For the simulations I attempted to follow hutchphd's example where instead of using an ammeter with 10 per cent error, I assumed that the current source has a 10 percent error on what the current is set at. Then a voltmeter with 2 percent accuracy is measuring the potential drop across the resistor.

 

[FactChecker]

There's no real experiment, so it's up to us. I mentioned a current source (not a voltage source), but we're not forced to focus on this. I am just wondering the sources of correlations between I and V in a real life experiment.
For the simulations I attempted to follow hutchphd's example where instead of using an ammeter with 10 per cent error, I assumed that the current source has a 10 percent error on what the current is set at. Then a voltmeter with 2 percent accuracy is measuring the potential drop across the resistor.

Thanks. That answers my question. So you are measuring a fixed, but unknown resistance using meters that have the errors you describe. The voltage and current errors are simply measurement errors that are independent of each other. That makes sense to me now. So your analysis and Monti Carlo simulation are about the distribution of the calculated resistance using Ohm's law with the measurement errors. I guess that the means of the MC voltage and current simulations are set for the specific true resistance. I would have to question whether the mean of a ratio is simply the ratio of the means.

 

[Stephen Tashi]

I would have to question whether the mean of a ratio is simply the ratio of the means.

Also, the ratio of two independent normally distributed random variables with zero means has a Cauchy distribution, whose mean does not exist. (I gather the idea is to estimate the true resistance as the mean of the V/I values.) The ratio of independent normals with non-zero means may be better behaved.

A paper by Marsaglia about dealing with the ratio of normal random variables is:

https://www.google.com/url?sa=t&rct...sg=AFQjCNEgO1dvktreWiL-rt-ZPcS3K1FmYQ&cad=rja

As to the merits of pencil-and-paper methods of "error propagation", my impression (based only on questions that appear in the forum about error propagation) is that (statistically!) instruction in the pencil and paper methods seems to teach a set of procedures, but does not connect those procedures with the theory of probability models. Many questioners ask about how to compute "uncertainties" in things and are confident that "uncertainty" has an obvious meaning. It may indeed have a well defined meaning in their particular technical discipline, but I don't detect this meaning is identical to a particular concept in probability and statistics. Of course, there is a potential bias in my sample since people with less understanding of the subject would be more inclined to ask questions about it.

 

[fluidistic]

Thanks. That answers my question. So you are measuring a fixed, but unknown resistance using meters that have the errors you describe. The voltage and current errors are simply measurement errors that are independent of each other. That makes sense to me now. So your analysis and Monti Carlo simulation are about the distribution of the calculated resistance using Ohm's law with the measurement errors. I guess that the means of the MC voltage and current simulations are set for the specific true resistance. I would have to question whether the mean of a ratio is simply the ratio of the means.

I think the median nails it pretty accurately. The mean is going to be biased towards greater values. Part of the reason why I asked why the GUM states to report the mean and SD rather than the median and confidence intervals.

 

[Stephen Tashi]

Part of the reason why I asked why the GUM states to report the mean and SD rather than the median and confidence intervals.

A simple argument for reporting the mean and SD:
Suppose we do N independent replications of a simulation and each replication produces one value of Y. Then, by the central limit theorem, the mean value of all the Y's is approximately normally distributed for large N , provided the distribution of Y (as an individual random variable) has finite variance. (The distribution of Y need not be a normal distribution for this to hold.) So if the purpose of doing the simulation is to estimate the "true" value Y by using the mean of the Y data, the estimated standard deviation of Y is relevant to computing confidence intervals.

In the above approach, the size of confidence intervals depends on the number of samples (replications) since that number enters into the calculation of the sample standard deviation of the Y data. By contrast, you suggest looking at a histogram and its median to compute a confidence interval. How does the size of this confidence interval depend on the number of replications you did to create the histogram? If the number you report is not a function of the number of replications of the simulation, then can it be interpreted as a "confidence interval" or should we use some other terminology for it?

 

[hutchphd]

Also, the ratio of two independent normally distributed random variables with zero means has a Cauchy distribution, whose mean does not exist.

These variables do not have zero means

 

[FactChecker]

The distribution of the ratio of uncorrelated normal variables with non-zero means is discussed here. They give the equation for the variance. It uses the individual means and variances. I do not see anything about the mean. It makes me tired.
This is something where I would feel more comfortable with the Monte Carlo simulation than with my analysis, and it really is a very basic thing.

 

[hutchphd]

Zero over zero is never fun.

 

[Stephen Tashi]

This is something where I would feel more comfortable with the Monte Carlo simulation than with my analysis, and it really is a very basic thing.

And the most basic thing, is: What is the problem being analyzed? The question highlights the distinction between the usual type of "confidence interval" analysis versus "error propagation" analysis.

In confidence interval analysis, we usually have data in the form of independent samples. The confidence interval analysis depends on the data and the amount of data we have.

By contrast, the example being simulated assumes some given distributions. There is no mention of how the parameters of these distributions relate to any data. It is as if the parameters of the distributions are handed to us and assumed to be exact.

The general form of confidence interval analysis is that we have a formula $\hat{c}$ for estimating some parameter $c$ of a distribution as a function of data. The usual form of a confidence interval is $( \hat{c} - L/2, \hat{c} + L/2)$ where $L$ is positive constant. A confidence interval depends on data that has randomness, so it is a randomly generated interval. The probability associated with confidence intervals of length $L$ is the probability that the true value of the parameter lies within at least one of these randomly generated intervals. (This probability is not associated with single confidence intervals. For example, a "95 % confidence" is not a probability that can be associated with a single interval like $(25.3 - L/2, 25.3 + L/2)$).

So how do the simulation results relate to a confidence interval analysis? I think the histogram of $V/I$ is relevant to analyzing whether a single measurement (a sample of size 1) of $(V,I)$ is within a certain distance of the true value of $R$. If multiple measurements are taken, further analysis is needed. However, the parameters of the distributions for $V,I$ used in the simulation results are not presented as estimates from data. It appears logically contradictory to analyze the situation of multiple $V/I$ measurements using a simulation that ignores them.

 

[FactChecker]

It's a very simple Monte Carlo simulation where the V and I measurements are modeled as Gaussian. I think that the sample results can be used for probability distributions and confidence intervals as with any other random sample. The validity of the model to represent the particular resistance problem might be questionable.

 

[Stephen Tashi]

It's a very simple Monte Carlo simulation where the V and I measurements are modeled as Gaussian. I think that the sample results can be used for probability distributions and confidence intervals as with any other random sample.

I agree that the simulation is simple. But what is the analysis? For example, what is the length of a 95% confidence interval centered on the mean ( or median if we prefer) of 10 pairs of $V/I$ measurements?

 

[FactChecker]

I guess I have to take back any strong statement about the confidence intervals. I would treat the Monte Carlo sample the same as any other statistical sample.
I am also troubled by an analytical approach that allows it to be a ratio of normal random variables. Suppose we ignore the problem of division by zero. What do we say if the voltage measurement is positive and the current measurement is negative? Or vice versa. Do we just throw out that possibility? And what if both happen to be negative? Since they are assumed to be uncorrelated, that would be possible. Would we treat that as more valid just because they are not mixed positive/negative and they give a positive resistance? This resistor problem is a hypothetical problem and I am not sure that we are modeling it properly.
The problem hurts my head. I think I will leave this problem to others.