SUMMARY
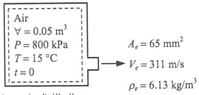
The discussion centers on the principles of mass conservation in a closed system, specifically addressing the expulsion of air and its impact on system mass. The participants clarify that while air is expelled, the total mass of the system remains unchanged due to the control volume concept. The relevant equation governing this phenomenon is presented as $$ \frac{d}{dt} m_{cv} = - \rho_e A_e V_e $$, emphasizing that the mass within the control volume can change over time while the overall system mass does not. The distinction between the system and control volume is crucial for understanding fluid dynamics in this context.
PREREQUISITES
- Understanding of control volume analysis in fluid dynamics
- Familiarity with mass conservation principles
- Knowledge of fluid properties such as density and velocity
- Proficiency in calculus, particularly with integrals and derivatives
NEXT STEPS
- Study the fundamentals of control volume analysis in fluid mechanics
- Learn about the Navier-Stokes equations and their applications
- Explore the concept of mass flow rate and its calculations
- Investigate the implications of the Reynolds Transport Theorem (R.T.T.) in fluid systems
USEFUL FOR
Students and professionals in engineering, particularly those specializing in fluid dynamics, thermodynamics, and mechanical engineering, will benefit from this discussion.