Quadratic functions: [Diagram Included] Football game scenario

[Swan]

Homework Statement

You are the quarterback for the Quinte Saints Football team. You are in the middle of the COSSA gold medal game and you see your receiver is wide open down the field beside the sideline. If he catches the ball, you win the game. However, the biggest guy Joey from the opposing team who is 190 cm tall is running towards you. You decide to throw the ball so that the highest part of the path is 1.5 m over Joey's head to avoid him reaching it if he jumps. You throw the ball at your receiver releasing the football at your head level when Joey is 5 m away from you.

The goal of this task is to figure out if your teammate can catch the ball and win the game.

Assumption variable: Your Height (to the nearest centimeter): 150 cm. **NOTE**: We had to assume what the quarterback's height was and in this my height is 150 cm.

a) Draw a sketch of the situation including the path of the ball (assume no wind). Fill in all information you know at this time.​

b) Determine the equation representing the path of the football.​

c) Your receivers typically catch the ball 1 m from the ground. If your player is 9.5 m away, and can run within 2 m of his initial location to catch the ball, does he catch the ball to win the game? Justify.​

Homework Equations

None

The Attempt at a Solution

a)

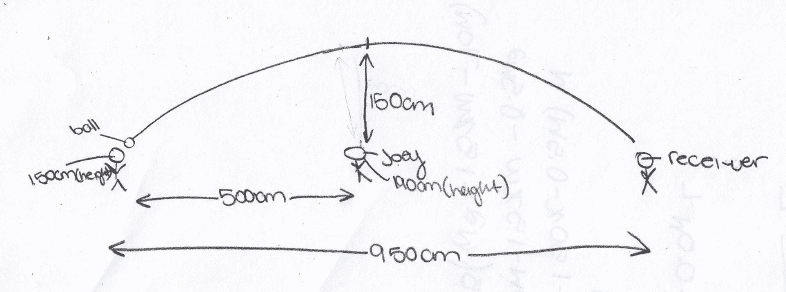
b) I have no idea how to go about this.​

c) I say he would catch the ball to win the game because the receiver can cover 2 m of horizontal distance if needed.​

 

[tms]

a) The diagram looks okay except that you left out the details of the receiver: the height and radius in which he can catch the ball.

b) Start by writing down the kinematics equations. Since you are not given Joey's speed, I think you can assume it is enough slower than the ball's speed that it can be ignored. You don't know the speed at which the ball is thrown, or the angle, but you do know where it has to be to avoid Joey, and approximately where it has to land to be caught. With that information it should be possible to find the solution.

c) You can't answer (c) until you find the equation in (b). It is possible that the ball speed needed to avoid Joey will be such that the ball won't land close enough to the receiver.

 

[Swan]

no information about the receiver is given and also no speed is given throughout this question

 

[tms]

You are told that the ball will be caught 1 m above the ground within 2 m of the receiver's initial position. Those conditions put some constraints on the initial velocity and angle of the ball. Without those constraints, if all you had to do was avoid the defender, you'd just have to use a very high speed and a high angle.