maguss182
- 16
- 0
- Homework Statement
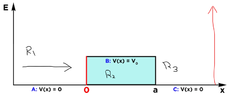
- Need to find what the boundary condition is for an Energy hitting an infinity wall of potential
- Relevant Equations
- Ce^ikx+De-ikx - Wavefunction for 3rd region I need to apply boundary conditions to.
I have the equations for all three regions but usually for region 3, which is Ce^ikx+De-ikx, the C term would be zero since there is no reflection, but with the infinite wall would it reflect? Would the whole wavefunction go to zero like when working with the infinite square wall? I'm stuck on this part, any help would be greatly appreciated
I edited this screenshot I took from a youtube video, to make it clearer what I'm referring too
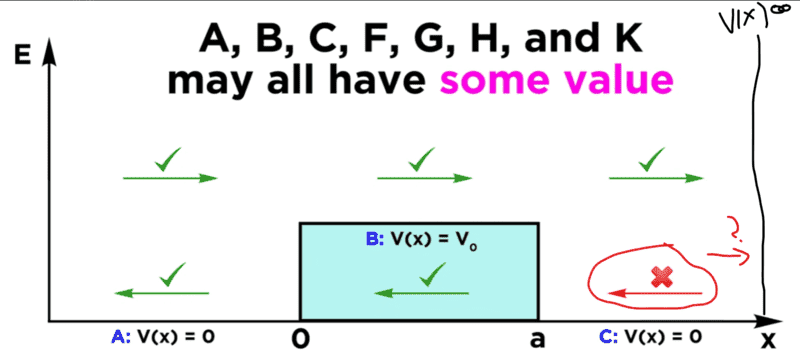
I edited this screenshot I took from a youtube video, to make it clearer what I'm referring too