Question about a boundary-value problem (electrostatics)

[Sum Guy]

Laplacian for polars:

$$\frac{1}{r}\frac{\partial}{\partial r}\left( r\frac{\partial \phi}{\partial r}\right) + \frac{1}{r^{2}}\frac{\partial^{2} \phi}{\partial \theta^{2}} = 0$$

This is in relation to a problem relating to a potential determined by the presence of a wedge shaped metallic conductor (see image).

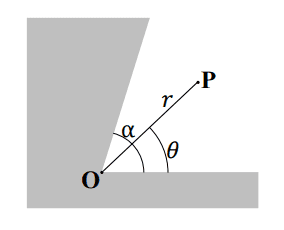
Working through the problem:

$$\phi (r,\theta) = R(r)\psi (\theta )$$ with $$R(r) \propto r^{v}$$ and Dirichlet boundary conditions $$\phi (r,0) = \phi (r,\alpha ) = V_{0}$$

Substituting into the Laplacian:
$$\frac{1}{r}\frac{\partial}{\partial r}\left( rvr^{v-1}\psi (\theta)\right) + \frac{1}{r^2}r^{v}\psi^{''}(\theta )$$
$$ = r^{v-2}\left( \psi^{''}(\theta ) + v^{2}\psi (\theta )\right) = 0$$
Therefore
$$\psi^{''}(\theta ) + v^{2}\psi (\theta ) = 0$$
Solution is of the form
$$\psi (\theta) = Acos(v\theta ) + Bsin(v\theta )$$
Applying BCs:
$$\phi (r,\theta ) = r^{v}\left(Acos(v\theta ) + Bsin(v\theta )\right)$$
$$\phi (r,0) = V_0 \rightarrow A = V_{0}r^{-v}$$
$$\phi (r,\alpha) = V_0 \rightarrow B = \frac{V_{0}r^{-v}(1-cos(v\alpha ))}{sin(v\alpha )}$$ ...which leaves me with utter crap.

However if we choose V₀ such that it is zero then we can reapply the BCs:
$$\phi (r,0) = V_0 \rightarrow A = 0$$
$$\phi (r,\alpha) = V_0 \rightarrow sin(v\alpha ) = 0 \rightarrow v = \frac{n\pi }{\alpha}$$

Resulting in a more pleasant $$\phi(r,\theta ) = Br^{\frac{n\pi }{\alpha}}sin(\frac{n\pi }{\alpha}\theta )$$

So there a few things here that I'm struggling to understand:
If I don't set V₀ = 0 then how can I solve the problem?
I should have a unique solution, yet B isn't determined?
How might I correct my solution so that the potential was V₀ on the boundaries?

 

[Twigg]

Notice you're short two boundary conditions to solve this problem. Add in $\phi(r,\theta) < \infty$ everywhere on the region of integration. First, test that condition as r goes to infinity: $\phi(r,\theta) < \infty$ as $r \to \infty$ implies $\nu \leq 0$. Second, test the same condition as r goes to zero: $\phi(r,\theta) < \infty$ as $r \to 0$ implies $\nu \geq 0$. Meaning, there's only one term in the solution: the 0th order term, simply $\phi(r,\theta)=A=V_{0}$, $\nu = 0$. The reason you didn't see it when you performed separation of variables is because $\nu = 0$ makes $\frac{\partial}{\partial r}\phi(r,\theta) = 0$. If you had handled the zeroth-order term separately, you would've gotten $\frac{\partial^{2}}{\partial\theta^{2}}\psi(\theta) = 0$, which implies $\frac{\partial}{\partial\theta}\psi(\theta) = \frac{\psi(\alpha) - \psi(0)}{\alpha}=\frac{V_{0} - V_{0}}{\alpha} = 0$. That tells you that $\psi(\theta) = \psi(0) = V_{0}$.

 

[Sum Guy]

Notice you're short two boundary conditions to solve this problem. Add in $\phi(r,\theta) < \infty$ everywhere on the region of integration. First, test that condition as r goes to infinity: $\phi(r,\theta) < \infty$ as $r \to \infty$ implies $\nu \leq 0$. Second, test the same condition as r goes to zero: $\phi(r,\theta) < \infty$ as $r \to 0$ implies $\nu \geq 0$. Meaning, there's only one term in the solution: the 0th order term, simply $\phi(r,\theta)=A=V_{0}$, $\nu = 0$. The reason you didn't see it when you performed separation of variables is because $\nu = 0$ makes $\frac{\partial}{\partial r}\phi(r,\theta) = 0$. If you had handled the zeroth-order term separately, you would've gotten $\frac{\partial^{2}}{\partial\theta^{2}}\psi(\theta) = 0$, which implies $\frac{\partial}{\partial\theta}\psi(\theta) = \frac{\psi(\alpha) - \psi(0)}{\alpha}=\frac{V_{0} - V_{0}}{\alpha} = 0$. That tells you that $\psi(\theta) = \psi(0) = V_{0}$.

Thank you for your reply.

Wouldn't that lead to the conclusion that $\phi (r,\theta ) = V_{0}$ everywhere? The solution must have some $r$ dependence..? Shouldn't the solution be of the form that I provided when $V_{0} = 0$?

 

[Twigg]

If having the unbounded powers of r weren't an issue, you'd have a superposition of solutions like you got for different values of n, plus the constant $V_{0}$. There wouldn't be a unique solution because you're still short at least one boundary condition for r at infinity.

 

[TSny]

$$\phi (r,0) = V_0 \rightarrow A = V_{0}r^{-v}$$

$A$ is required to be a constant in the process of solving by separation of variables. It cannot be a function of $r$.

When you write $R(r) = r^{\nu}$, you are not allowing for all possible forms of $R(r)$.

I suggest you go back through the process of separation of variables to find the differential equation that $R(r)$ must satisfy and see if you can find a solution that is not of the form $r^{\nu}$.