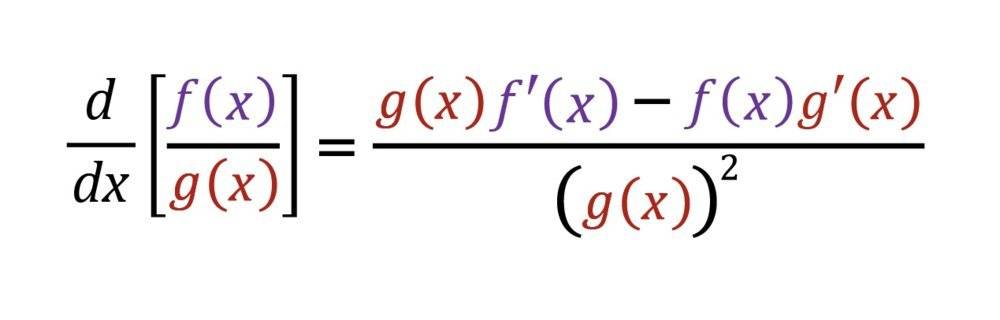Discussion Overview
The discussion centers around the quotient rule of derivatives, specifically exploring the rationale behind squaring the denominator function g(x) in the formula. Participants express a desire to understand the underlying reasons for the formula rather than just its application, delving into derivations and mnemonic devices related to the rule.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant questions why g(x) is squared in the denominator of the quotient rule, seeking a deeper understanding of its origin.
- Another suggests deriving the quotient rule using the product and chain rules as a way to clarify the reasoning behind the formula.
- A participant explains that the squaring arises from the differentiation of x^n, specifically when n = -1, leading to a squared term in the denominator.
- Some participants share their struggles with remembering the order of terms in the numerator and suggest using the product rule as an alternative approach.
- One participant introduces a mnemonic device to help remember the terms in the quotient rule, emphasizing the structure of the formula.
- A later reply discusses the definition of the derivative and how the common denominator leads to the squared term in the limit process.
- Another participant finds a particular explanation intuitive and notes that understanding the numerator requires similar reasoning as the product rule.
- A participant shares a rhyme to aid in memorizing the quotient rule, highlighting the squared denominator as a key component.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and approaches to the quotient rule, with no consensus on a singular explanation for why g(x) is squared. Multiple competing views and methods for understanding the rule remain present in the discussion.
Contextual Notes
Some participants reference derivations and proofs from external sources, indicating that the discussion may depend on different interpretations of mathematical principles and definitions. There are unresolved aspects regarding the clarity of the quotient rule's derivation and its mnemonic devices.