woody stanford
- 26
- 4
The question I have is regarding the time-variant form of Schrödinger's equation. Can I just put a complex number of form c=a+bi where the i is in it or can I just literally put sqrt(-1) where the i is:
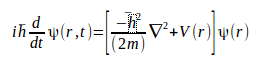
addendum: sorry forgot the t in the right-hand term, it should read (r,t) instead of (r)
Also any comments/insights on some of the other terms in it would be welcomed (as I'm writting a c program to inject various values into it) and would appreciate the help.
Was thinking if I could just put a+bi in there that to put it back to i all I would have to do is set (real)a=0 and (imaginary)b=1
addendum: sorry forgot the t in the right-hand term, it should read (r,t) instead of (r)
Also any comments/insights on some of the other terms in it would be welcomed (as I'm writting a c program to inject various values into it) and would appreciate the help.
Was thinking if I could just put a+bi in there that to put it back to i all I would have to do is set (real)a=0 and (imaginary)b=1
Last edited: