Questions about cancelation of induced EMF and minimizing eddy currents

[artis]

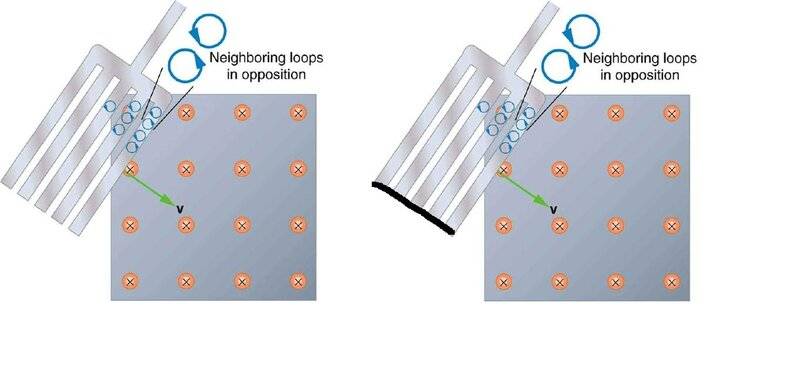
I recalled a drawing that was provided in an EM text. Without going in length, the basics is simple - in order to minimize eddy currents one divides up a planar surface area of a wide conductor into small separate sections. As is done in transformer core laminations for example.
In the image a fork like conductor is shown, but I copied and duplicated the original image on the left and added a black connection at the bottom, how would that change the situation?
Now the fork is made up of multiple identical rectangular loops, but all loops share one common conductor that means, I think, that as long as there is EMF induced in at least two neighboring loops it should cancel out due to the opposite current directions that have to go through the same shared conductor?

The only time EMF would not be canceled is when the changing B field exists only within one of the smaller loops as far as I think, and it would only be partially cancelled if the EMF in adjacent loops would be different in magnitude.

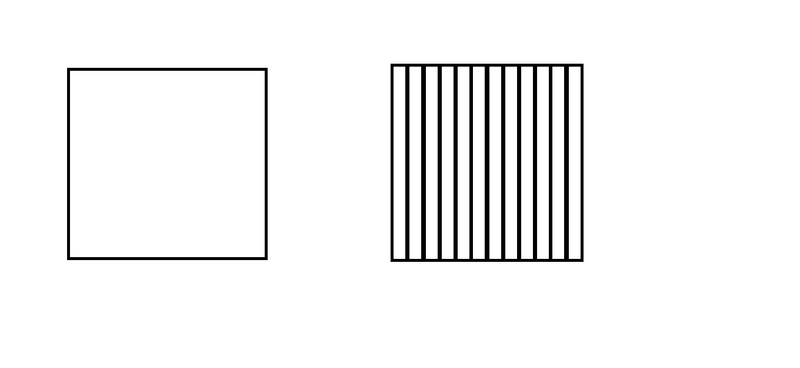
Now a second example I wish to ask is this, imagine in this case the loop is stationary and so is the field , it's still a AC field. Now on the left side there is a single rectangular loop, the field passes through it and current is induced in the loop, so far so good.
On the right side there is a rectangle that consists of multiple identical rectangular loops, all again sharing a common side wire.
Is there current induced in the right sided rectangular loop containing multiple loops?
And if so then is it induced in the smaller loops or just the overall outermost loop?
Assume a symmetrical and even flux through the loop area to simplify the question.
My own guess would be that current induction should cancel not just in the smaller loops but also in the outermost loop, because the outermost loop cannot have current through it independently of the smaller loops, given the smaller loops work to cancel the applied flux?

 

[hutchphd]

My own guess would be that current induction should cancel not just in the smaller loops but also in the outermost loop, because the outermost loop cannot have current through it independently of the smaller loops, given the smaller loops work to cancel the applied flux?

Not sure I understand. Unlike the "open" fork, in the limit the "closed" fork is essentially just a conductor. So there would be no large scale eddy currents in a conductor?

 

[artis]

Not sure I understand. Unlike the "open" fork, in the limit the "closed" fork is essentially just a conductor. So there would be no large scale eddy currents in a conductor?

Its not about whether the conductive piece of metal is part of a larger circuit not shown, it is only about how much , if any, current can be induced , and how much, if any, can be canceled from an applied external flux cutting a piece of conductive material in a shape like that shown.
I don't think (maybe I'm wrong) that say if you had a thin but wide planar like conductor that passed current along it being a piece of wire within a circuit that this would make any difference in the magnitude of eddy currents induced within the flat conductor if an external AC magnetic field was cutting it perpendicularly.

A metal like copper has lots of free electrons that can drift within it so I would think such a conductor could support both directional current flow as part of a larger circuit as well as circular current flow that would arise from an applied perpendicular to surface field.
But it does raise in interesting question, would such a scenario shift the directional current to one side - that in which it coincides in the same direction as the eddy loop current...

Either way this is a side thought , the main thought I hope you now understand is just about externally applied field and induced current cancellation.

 

[artis]

Maybe some other members would have something to add?

 

[DaveE]

I'm not sure I fully understand your question, because it seems too simple. But...
Every conductor loop will have current induced from the B field. You can add (with vectors) the currents in conductors that are shared between loops. With perfect symmetry, the inner conductor currents cancel, but not in the outer loop. Of course there are a whole bunch of assumptions going on here (superconductors, uniform fields, etc.).