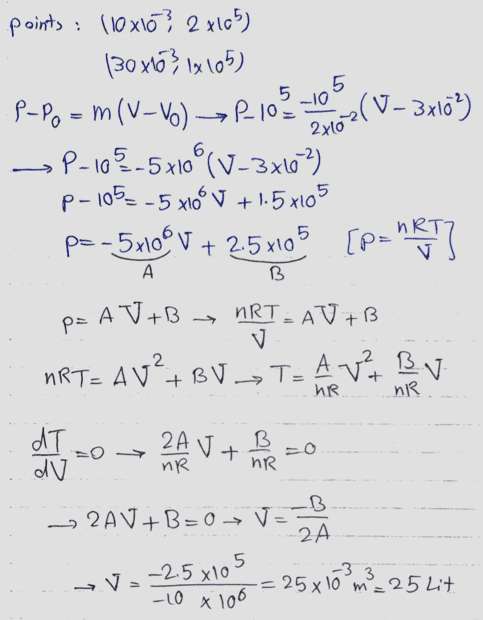Question's Diagram: Am I Right?

  • Thread starter Thread starter MatinSAR
  • Start date Start date
  • Tags Tags
    Diagram
Click For Summary

Homework Help Overview

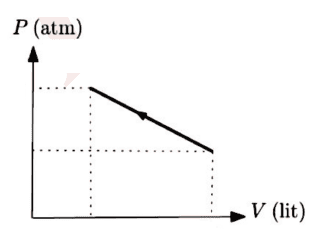
The discussion revolves around a diagram related to the condensation of an ideal gas, with participants questioning the accuracy of the diagram and the terminology used. There is a focus on understanding the implications of the diagram in the context of thermodynamics.

Discussion Character

  • Exploratory, Conceptual clarification, Assumption checking

Approaches and Questions Raised

  • Participants discuss the correctness of the diagram and whether it represents a maximum or minimum. There are questions about the appropriate terminology, specifically the use of 'condense' versus 'compress'. Some participants suggest using non-SI units for simplicity and explore the implications of the gradient of the line in the diagram.

Discussion Status

The discussion is active, with participants providing feedback on the diagram and terminology. Some guidance has been offered regarding the use of units and the need to verify whether the point in question is a maximum or minimum. There is an acknowledgment of the need for clarity in language and concepts.

Contextual Notes

Participants are navigating potential language barriers and the appropriateness of unit systems in the context of the problem. There is a mention of a derivative test being considered to analyze the maximum or minimum nature of the point in question.

MatinSAR
Messages
673
Reaction score
204
Homework Statement
We condense some ideal gas from a volume of 30 liters and a pressure of 1 atmosphere to a volume of 10 liters and a pressure of 2 atmospheres. What is the volume of the gas when its temperature is maximum?
Relevant Equations
pV=nRT
Hello. This is question's diagram.
1674331087276.png

Can someone tell me if I am wrong ?

1674332589798.png
 
Physics news on Phys.org
Looks ok, except that you did not check that it is a maximum. Could be a local minimum, in which case either the starting or finishing temperature would be the max.
 
Reply
  • Like
Likes   Reactions: MatinSAR
MatinSAR said:
Homework Statement:: We condense some ideal gas
Presumably you mean 'compress'. 'Condense' means something different!

In addition to what @haruspex already said...

It's not necessary to use SI units here. You can work in 'atm' and 'lit' (though 'lit' is not a common abbreviation for litres) and you will get the same answer. It's less messy.

For example, the gradient of the line can immediately be written as ##\frac {-1}{20}## (corresponding to units of atm/lit).

Try it – and check you understand why it works here.
 
Reply
  • Like
Likes   Reactions: MatinSAR
haruspex said:
Looks ok, except that you did not check that it is a maximum. Could be a local minimum, in which case either the starting or finishing temperature would be the max.
I will use derivative test to prove it.
Thanks a lot for your help.
Steve4Physics said:
Presumably you mean 'compress'. 'Condense' means something different!
Sorry! I haven't spoken English for a long time and I didn't remember the correct word so I used google translate ...
Steve4Physics said:
It's not necessary to use SI units here. You can work in 'atm' and 'lit' (though 'lit' is not a common abbreviation for litres) and you will get the same answer. It's less messy.
Yes, thanks, I use SI units when I'm not sure if it's correct to use non-SI units.
Steve4Physics said:
For example, the gradient of the line can immediately be written as −120 (corresponding to units of atm/lit).

Try it – and check you understand why it works here.
Thanks a lot for your help ...
I will try this and I hope I will get similar result.
 
Reply
  • Like
Likes   Reactions: Steve4Physics

Similar threads

Why are moments not included in free body diagrams?
  • · Replies 31 ·
2
Replies
31
Views
2K
Force diagram for integrated exercise
  • · Replies 9 ·
Replies
9
Views
2K
Falling hailstones hitting two car windscreens
  • · Replies 23 ·
Replies
23
Views
1K
Phase difference between two light waves of the same frequency
  • · Replies 12 ·
Replies
12
Views
1K
Is the Charge Conservation Correct in This Meson Decay Feynman Diagram?
  • · Replies 8 ·
Replies
8
Views
1K
Time taken to slide down a circular path (with friction)
  • · Replies 43 ·
2
Replies
43
Views
3K
Is it friction or tension acting on the person hanging on a rope?
  • · Replies 4 ·
Replies
4
Views
1K
Question about Feynman diagram showing annihilation
  • · Replies 4 ·
Replies
4
Views
888
Spherical pendulum confusion [Issue resolved]
  • · Replies 2 ·
Replies
2
Views
669
Airplane Vector Problem: Drawing the diagram
  • · Replies 10 ·
Replies
10
Views
2K