Quick question about binomial theorem

[MadmanMurray]

I know how to expand binomials with the aid of pascals triangle and also with the aid of the nCr function on the calculator. I'm not quite sure about this formula though

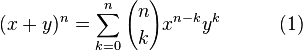
see the part in the brackets where n is above k. What does that mean? Someone told me that represents nCk. Is that true? Are you supposed to use that nCr function when using the binomial theorem to expand binomials? I was under the impression that the formula worked out the coefficients without using that nCr function.

 

[lurflurf]

yes the part in the brackets where n is above k is nCk
also expressible as
n!/[(n-k)!n!]

 

[MadmanMurray]

Thanks a lot. I thought that formula was some complex way of getting the binomial coefficients without using the nCr button on the calculator. On a test I had a question that asked me to expand a degree 5 binomial using the binomial theorem and I was thinking the teacher wouldn't make us waste our time using that nCr button so many times. I used it anyway so I musta got the question right.

 

[mathman]

yes the part in the brackets where n is above k is nCk
also expressible as
n!/[(n-k)!n!]

You have a typo? should read n!/[(n-k)!k!]

 

[lurflurf]

You have a typo? should read n!/[(n-k)!k!]

yes

yes the part in the brackets where n is above k is nCk
also expressible as
n!/[(n-k)!k!]