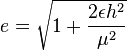SUMMARY
The discussion centers on the interpretation of the formula for orbital eccentricity (e) in relation to specific mechanical energy and angular momentum in celestial mechanics. It confirms that e is indeed dependent on the specific mechanical energy of a celestial body, such as a planet orbiting the Sun, as well as its angular momentum. The context provided includes definitions of specific orbital energy, the standard gravitational parameter, and the concept of reduced mass, which is crucial for understanding the two-body problem in gravitational physics.
PREREQUISITES
- Understanding of specific mechanical energy in orbital dynamics
- Familiarity with angular momentum concepts in physics
- Knowledge of gravitational forces and their mathematical representation
- Basic grasp of the two-body problem and reduced mass calculations
NEXT STEPS
- Research the derivation of the formula for specific orbital energy in celestial mechanics
- Learn about the standard gravitational parameter and its applications in orbital calculations
- Explore the implications of angular momentum conservation in orbital dynamics
- Study the two-body problem in detail, focusing on reduced mass and its significance
USEFUL FOR
Astronomy students, physicists, and engineers involved in orbital mechanics and celestial navigation will benefit from this discussion.