- #1
iris_m
- 8
- 0
rather urgent :(, isomorphic graphs, planar graph
I need help with the following two problems:
1) Is this graph planar?
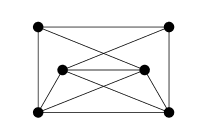
2) Are these two graphs isomorphic?
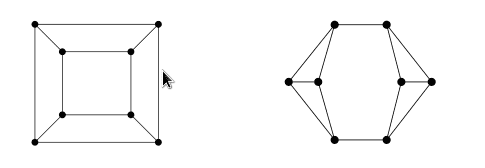
I don't know what to do with these two problems, and I would be really grateful for all your hits and help.
For number 1, I've tried to use the corollaries of Euler's formula, but that gives me nothing, and for number two, I think it has something to to with the fact that one graph has a cycle of order 3, and the other one does not, but I don't know how to prove that isomorphisms preserve k-cyles. :(
Also, the first graph is bipartite, and the other one is not. Does isomorphism preserve this?
Please, help.
I need help with the following two problems:
1) Is this graph planar?
2) Are these two graphs isomorphic?
I don't know what to do with these two problems, and I would be really grateful for all your hits and help.
For number 1, I've tried to use the corollaries of Euler's formula, but that gives me nothing, and for number two, I think it has something to to with the fact that one graph has a cycle of order 3, and the other one does not, but I don't know how to prove that isomorphisms preserve k-cyles. :(
Also, the first graph is bipartite, and the other one is not. Does isomorphism preserve this?
Please, help.