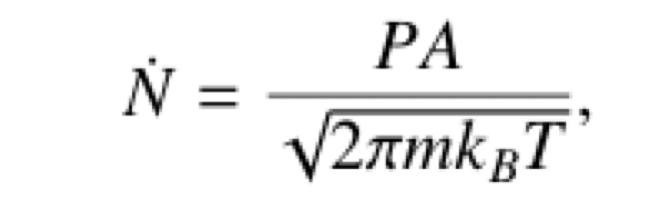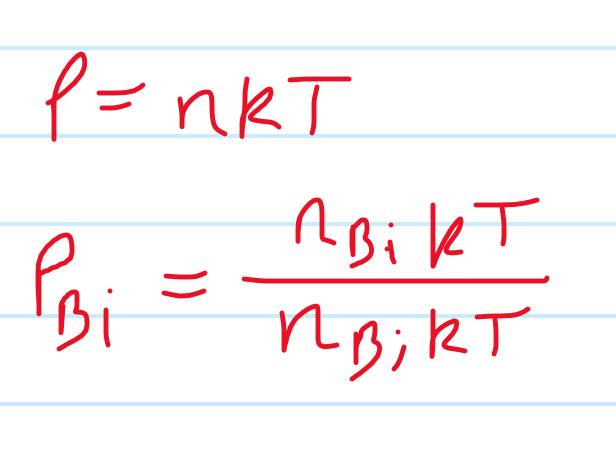Ratio of partial pressures of gas

[so_gr_lo]

Homework Statement

Bismuth is heated to 1100 K in an oven and gives rise to a beam of vapour molecules effusions from an aperture of area 10^-6 m^2. The beam contains Bi and Bi2 molecules in the ratio 1.41:1. Calculate the ratio of the partial pressures of Bi to Bi2 molecules

I believe the total pressure is the sum of the partial pressures but I’m not sure what to do with that, so I tried just calculating the ratio of the pressures but don’t know where to go from there

Relevant Equations

P=nKT where n is the number density per unit volume

and rate of effusion formula given below

Rate of effusion

 

[haruspex]

Just guessing here, but try writing your rate of effusion equation for each species separately. Each has its own pressure, mass and effusion rate, but they have the same temperature and area.

 

[so_gr_lo]

So this is what I get. since the rate of effusion is proportional to the number of molecules I guess you just plug the given number ratio and masses in and solve for the pressure ratio.

 

[haruspex]

So this is what I get. since the rate of effusion is proportional to the number of molecules I guess you just plug the given number ratio and masses in and solve for the pressure ratio.

View attachment 301449

That's what I had in mind, yes. And you know $N_{B_i}/N_{B_{i2}}, m_{B_i}, m_{B_{i2}}$.