cherry
- 25
- 6
- Homework Statement
- Find the interval of convergence for the given power series.
- Relevant Equations
- N/A
Hi, I'm having difficulty understanding why the interval of convergence is (0, 18].
When I tested x=18, I got the following conclusion using the ratio test.
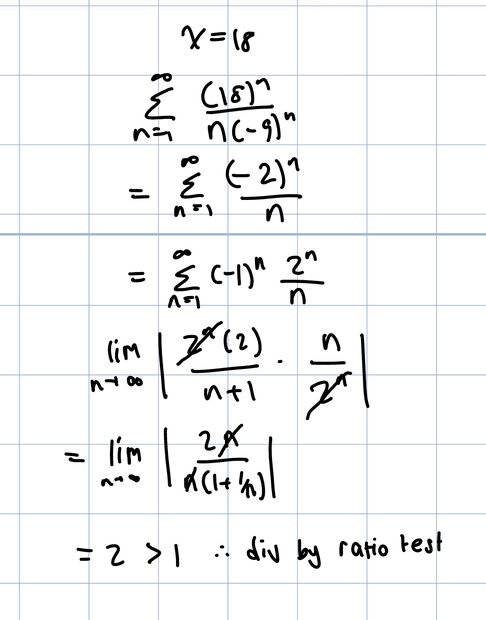
When I attempt using AST, the function still diverges as the lim (n -> inf) = 2^n / n ≠ 0.
What am I missing?
Thanks!
When I tested x=18, I got the following conclusion using the ratio test.
When I attempt using AST, the function still diverges as the lim (n -> inf) = 2^n / n ≠ 0.
What am I missing?
Thanks!
