Reaction temperature to maximize selectivity of product

[gfd43tg]

Hello,

I am confused a little bit on why for a reaction with a given activation energy, one should run at high temperatures if the activation energy of the desirable product, D, is greater than the undesirable product, U.

To illustrate this, I have an example with two reactions
$A + B \rightarrow D$
$A + B \rightarrow U$

$r_{D} = 10 \hspace{0.05 in} exp(- \frac {8000}{T})C_{A}C_{B}$
$r_{U} = 100 \hspace{0.05 in} exp(- \frac {1000}{T})C_{A}^{1/2}C_{B}^{-3/2}$

So I know to maximize the selectivity here, I will want to use a high concentration of A and low concentration of B, so I will use a semibatch reactor with a slow feed of B. However, as far as temperature is concerned, I am a little bit stumped. Why is it that increasing the temperature will help the desirable product formation? exp(-8000/T) is going to be much smaller than exp(-1000/T).

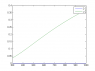
I run it in MATLAB and I see that the desirable is a flat line, so the difference between the two is actually increasing as temperature increases, so the undesirable reaction is increasing much faster than the desirable reaction rate as temperature increases. That means $r_{U}$ is growing a lot quicker with temperature increase than $r_{D}$, which seems to be the opposite of what I want to accomplish.

T = linspace(300,1000,1e4);
fD = @(T) exp(-8000./T);
fU = @(T) exp(-1000./T);
plot(T,fD(T),T,fU(T))
legend('D','U')

 

[mfb]

exp(-8000/T) is going to be much smaller than exp(-1000/T).

True, but the ratio of the two depends on temperature. Just plug in two different values and calculate the ratio.

Your plot does not allow to see that as D is too low. Maybe use a logarithmic plot or directly plot the ratio.

 

[Chestermiller]

Hello,

I am confused a little bit on why for a reaction with a given activation energy, one should run at high temperatures if the activation energy of the desirable product, D, is greater than the undesirable product, U.

To illustrate this, I have an example with two reactions
$A + B \rightarrow D$
$A + B \rightarrow U$

$r_{D} = 10 \hspace{0.05 in} exp(- \frac {8000}{T})C_{A}C_{B}$
$r_{U} = 100 \hspace{0.05 in} exp(- \frac {1000}{T})C_{A}^{1/2}C_{B}^{-3/2}$

So I know to maximize the selectivity here, I will want to use a high concentration of A and low concentration of B, so I will use a semibatch reactor with a slow feed of B. However, as far as temperature is concerned, I am a little bit stumped. Why is it that increasing the temperature will help the desirable product formation? exp(-8000/T) is going to be much smaller than exp(-1000/T).

Yes. But it increases with temperature (percentage-wise) much more rapidly than exp (-1000/T)

I run it in MATLAB and I see that the desirable is a flat line, so the difference between the two is actually increasing as temperature increases, so the undesirable reaction is increasing much faster than the desirable reaction rate as temperature increases. That means $r_{U}$ is growing a lot quicker with temperature increase than $r_{D}$, which seems to be the opposite of what I want to accomplish.

Are you sure of your calculations? This should not happen: The ratio of D to U should increase with temperature for a given total product of U + D. That's in the mathematics.

Chet