- #1
binbagsss
- 1,254
- 11
Hi
I'm sure i understood this a week or so ago, and I've forgot the idea now. I'm just really confused, again, how you read the commutator relationships of from the action ?
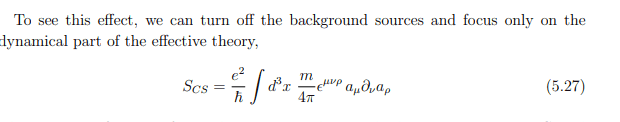

many thanks
(source http://www.damtp.cam.ac.uk/user/tong/qhe/five.pdf)
I'm sure i understood this a week or so ago, and I've forgot the idea now. I'm just really confused, again, how you read the commutator relationships of from the action ?
many thanks
(source http://www.damtp.cam.ac.uk/user/tong/qhe/five.pdf)