evinda
Gold Member
MHB
- 3,741
- 0
Hello!
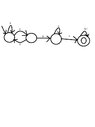
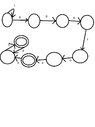
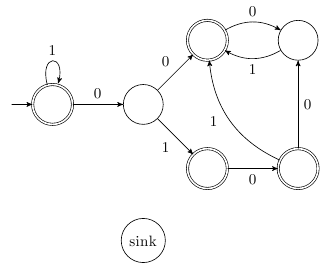
I have to draw the DFA of the language of the following expressions:
a){1^*\{00,010,\varnothing\}(01)^{*}}
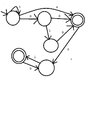
b)(\{\{1,0\}^{*},(\varnothing,2)^*\})^{*}
Could you help me to find the languages that are meant,so I can draw the DFAs?
I have to draw the DFA of the language of the following expressions:
a){1^*\{00,010,\varnothing\}(01)^{*}}
b)(\{\{1,0\}^{*},(\varnothing,2)^*\})^{*}
Could you help me to find the languages that are meant,so I can draw the DFAs?