Reid's question at Yahoo Answers regarding related rates

[MarkFL]

Here is the question:

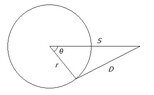
How fast is the distance between the friend changing when the distance between them is 210m?

A runner sprints around a circular track of radius 130 m at a constant speed of 4 m/s. The runner's friend is standing at a distance 210 m from the center of the track. How fast is the distance between the friends changing when the distance between them is 210 m? Round the result to the nearest thousandth if necessary.

a.
3.752 m/s
b.
3.757 m/s
c.
5.014 m/s
d.
3.804 m/s
e.
3.832 m/s

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Reid,

Let's work this problem in general terms, derive a formula, and then plug in the given data.

Let $S$ be the distance of the spectator from the center of the track, $r$ be the radius of the circular track, $D$ be the distance between the runner and the spectator and $v$ be the speed of the runner.

Please refer to the following diagram:

View attachment 893

We see, using the law of cosines, that we may state:

(1) \(\displaystyle D^2=r^2+S^2-2rS\cos(\theta)\)

Differentiating with respect to time, we find:

\(\displaystyle 2D\frac{dD}{dt}=2rS\sin(\theta)\frac{d\theta}{dt}\)

\(\displaystyle \frac{dD}{dt}=\frac{rS}{D}\sin(\theta)\frac{d \theta}{dt}\)

Now, since the distance the runner has covered is \(\displaystyle d=r\theta\) and the relationship between distance, constant velocity and time is \(\displaystyle d=vt\) we may state:

\(\displaystyle vt=r\theta\)

Differentiating with respect to time $t$, we have:

\(\displaystyle v=r\frac{d\theta}{dt}\)

Hence:

\(\displaystyle \frac{d\theta}{dt}=\frac{v}{r}\)

And so we may state:

\(\displaystyle \frac{dD}{dt}=\frac{Sv}{D}\sin(\theta)\)

We also have via Pythagoras and (1):

\(\displaystyle \sin(\theta)=\pm\sqrt{1-\cos^2(\theta)}=\pm\frac{\sqrt{\left((r+S)^2-D^2 \right)\left(D^2-(r-S)^2 \right)}}{2rS}\)

And so we may state:

\(\displaystyle \left|\frac{dD}{dt} \right|=\frac{v\sqrt{\left((r+S)^2-D^2 \right)\left(D^2-(r-S)^2 \right)}}{2Dr}\)

Plugging in the given data, we find in meters per second:

\(\displaystyle v=4,\,r=130,\,S=210,\,D=210\)

\(\displaystyle \left|\frac{dD}{dt} \right|=\frac{4\sqrt{\left((130+210)^2-210^2 \right)\left(210^2-(130-210)^2 \right)}}{2\cdot210\cdot130}=\frac{2\sqrt{1595}}{21}\approx3.803566770993497\)

Hence, the correct answer is d), rounded to the nearest thousandth.