Related rates (prism with a trapezoid base)

[starstruck_]

Homework Statement

A trough is 10 m long and a cross-section has the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has a height of 50 cm. If the trough is being filled with water at the rate of 0.2m³/min, how fast is the water level rising when the water is 30 cm deep?

I feel like I'm missing a connection or a relation between what I'm given here, or just don't know how to proceed with this problem.

Homework Equations

volume = (a+b)/2*h

The Attempt at a Solution

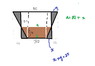
So I drew out an image and uh this about as far as I got with this :(

(I hope you can see that, not sure if it worked)

I am not sure what my next step should be. So, I know that the top of the trapezoid will change, the height of the trapezoid that I'm finding the derivative for is 30, and the top of the trapezoid changes as the water level rises, I also know that the bottom stays the same and is 25 cm smaller than the top from both sides. Not sure what my next step should be or what connection I'm missing.

**The number at the very top is an 80!EDIT: I think I just found another connection - I have similar triangles. There's a large one with a height of 50 and base of 25, and a small one with a base of x and height of 30? Right?

 

[LCKurtz]

Assuming the brown represents the water, label the depth of the water $h$ instead of $30$. You don't put the $30$ in until the end. Your next step should be to write the volume of the water in terms of just $h$. Come back when you have done that.

 

[starstruck_]

Assuming the brown represents the water, label the depth of the water $h$ instead of $30$. You don't put the $30$ in until the end. Your next step should be to write the volume of the water in terms of just $h$. Come back when you have done that.

the volume of the water in terms of h would be
v= (top+bottom)/2*h*l
v= 1000(top+bottom)/2*h
v= 500(top+bottom)*h

do I use the similar triangles to help me calculate the measurement for the bottom and find the derivative for my expression of the volume? (hoping what I wrote and my similar triangles are correct)

 

[LCKurtz]

the volume of the water in terms of h would be
v= (top+bottom)/2*h*l
v= 1000(top+bottom)/2*h
v= 500(top+bottom)*h

do I use the similar triangles to help me calculate the measurement for the bottom and find the derivative for my expression of the volume? (hoping what I wrote and my similar triangles are correct)

I would use similar trapezoids not similar triangles. But you need to explain where the $1000$ comes from (never mind, I just noticed the different units) and put in the values for top and bottom. You want $v = f(h)$ and remember, $v$ is the volume of the water, which varies with $h$.
(Edited).