Relationship between flow and pressure in a valve

[MaHo12345]

TL;DR

I am trying to identify the relationship between pressure and flow in a proportional valve, considering the flow conditions.

Hi,

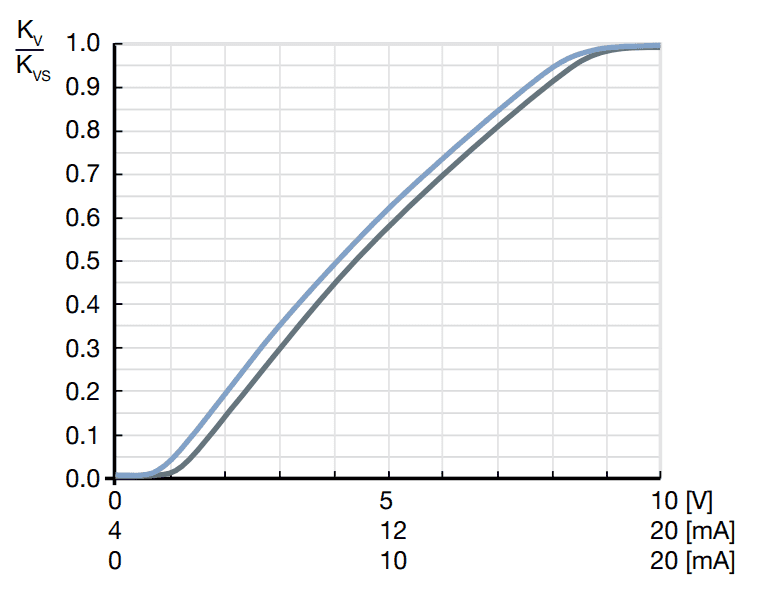
I have a valve which is connected to a pipe on both sides. I measure the pressure upstream of the valve. Downstream of the valve is a screw pump. I control my valve using an analog voltage input between 0 and 10 volts. According to the datasheet, the relationship between the analog input and $\frac{K_v}{K_{vs}}$ is as follows.

I also plotted the relationship between the voltage and the pressure upstream of the valve and got the following curve

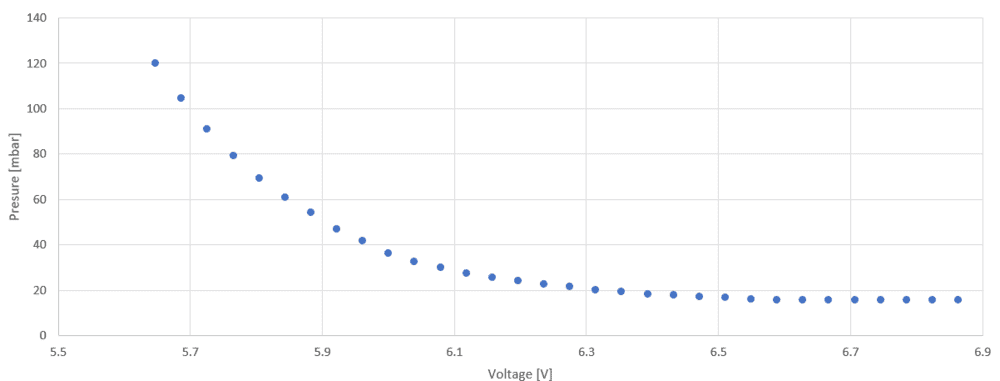
As visible, the pressure does not increase the same way as $\frac{K_v}{K_{vs}}$. My questions to this are as follows:

1. What is actually plotted in the first plot? Does this $\frac{K_v}{K_{vs}}$ correspond to orifice size? In this case, I am correct to say that the flow rate increases linearly with the voltage applied to the valve?
2. Why do I get the pressure-voltage relationship as show in the second curve? What would be the mathematical relationship describing this behaviour?

I have already had a few thoughts, however I could not recreate the behaviour of the second graph. I think I must calculate the $K_{vs}$ value for each specific pressure drop. However, I only know the pressure drop (as I measure it) but I do not know the flow rate. Can anybody point me in the right direction?

 

[Baluncore]

Can anybody point me in the right direction?

There are still too many possibilities.

What is the fluid. Hydraulic or pneumatic, liquid or gas ?

Why does a positive displacement pump follow a proportional valve ?
Or have we got that backwards ?

I would expect the flow rate to be determined by the pump.
What is the source of fluid to the valve inlet ?

Can you please give a link to the proportional valve data sheet.

 

[MaHo12345]

The fluid is air at room temperature. The pressure is negative (i.e. below atmosphere), that is why the scroll pump is connected downstream. As I understand, the flow decreases as the valve is closed (since it is not a hydraulic positive displacement pump with flow independent of pressure)

Source is atmosphere.

Link to the valve.

 

[Baluncore]

I also plotted the relationship between the voltage and the pressure upstream of the valve and got the following curve

The pressure upstream of the valve should be atmospheric pressure, less the pressure drop in the inlet filter and pipe, something that has not yet been specified.

 

[Baluncore]

Section 6, on page 7 (of the English data sheet) gives the meaning of K as the flow coefficient. Q is the flow.

 

[MaHo12345]

Sorry, let me specify:
The entire setup is (from upstream to downstream):
1. Inlet at atmospheric conditions
2. Needle valve set such that the pressure is 16 mbar(abs) when proportional valve (3) is fully opened
3. Proportional valve, controlled with 0-10V DC
4. Scroll pump
5. Outlet at atmospheric conditions

So i started from the formula in the data sheet which is

$$K_\mathrm{v} = \frac {Q_\mathrm{N}} {514} \cdot \sqrt {\frac {T_1 \rho_\mathrm{N}} {p_2 \cdot \Delta p} }$$

for the sub-critical case. I used the following values:
$Q_\mathrm{N}=2 \frac {\mathrm{l}}{\mathrm{min}} = 0.12 \frac {\mathrm{m^3}}{\mathrm{s}}, \ \rho_\mathrm{N}=1.293 \frac{\mathrm{kg}}{\mathrm{m^3}}, T_1 = 298 \ \mathrm{K}, p_2 = 0.016 \ \mathrm{bar}$ and for $\Delta p = p_1-p_2$ I inserted the measured values for $p_1$. For some pressure values I also considered the supercritical case, as indicated in the data sheet.

This left me with the following curve, which is not at all linear as I think it should be:
$K_\mathrm{vs} = 0.320 \frac {m^3}{h}$ (water) for this particular valve.

PS: I noticed that the x-axis with the voltage in the original post was wrong, I revised this now.