Relative-Motion analysis between two particles

[VinnyCee]

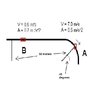
At the instant shown, the bicyclist shown at A is traveling at 7 m/s around the curve while increasing his speed at 0.5 m/s^2. The bicyclist at B is traveling at 8.5 m/s along the straight-a-way and increasing his speed at 0.7 m/s^2. Determine the relative vrlocity and the relative acceleration of A with respect to B at this instant.

http://img108.imageshack.us/img108/2137/engr204problem122012tn.jpg

I figured out the relative velocity:

$$\overrightarrow{V_B}\,=\,\left{(8.5)\,\widehat{i}\right}\,\frac{m}{s}$$

$$\overrightarrow{V_A}\,=\,\left{(7\,cos\,50)\,\widehat{i}\,+\,(-7\,sin\,50)\,\widehat{j}\right}\,\frac{m}{s}$$

$$\overrightarrow{V_{A/B}}\,=\,\overrightarrow{V_A}\,-\,\overrightarrow{V_B}$$

$$\overrightarrow{V_{A/B}}\,=\,\left{[\,(7\,cos\,50)\,-\,8.5]\,\widehat{i}\,+\,(-7\,sin\,50)\,\widehat{j}\right}\,\frac{m}{s}$$

$$\overrightarrow{V_{A/B}}\,=\,\left{(-4.00)\,\widehat{i}\,+\,(-5.36)\,\widehat{j}\right}\,\frac{m}{s}$$

$$V_{A/B}\,=\,\sqrt{(-4.00)^2\,+\,(-5.36)^2}\,=\,6.69\,\frac{m}{s}$$

The above answer for the magnitude of the velocity is correct. However, I cannot figure the acceleration part!

$$(A_A)_N\,=\,\frac{V_A^2}{\rho}\,=\,\frac{7^2}{50}\,=\,0.98\,\frac{m}{s^2}$$

I know the normal part of the bike at A's acceleration, but when I use this and the other EQ's for the acceleration, I don't get the correct answer! Please Help!

$$a_B\,=\,a_A\,+\,a_{B/A}$$

 

[andrevdh]

The radial part of the acceleration of A, $$a_r$$ is given by
$$\frac{v^2}{r}$$ while the tangential acceleration of A is $$a_t\ =\ 0.5\ m/s^2$$ which will itself be normal to the indicated radius. This means that you need to decompose both these accelerations into x- and y-components to get the components of the acceleration of A. Much less work need to be done if you rather align your x/y axis with these two acceleration components $$a_r , a_t$$ and express the acceleration of B in this sytem.

 

[VinnyCee]

Thanks for the help!

I set up the coordinate system like you said and get the right answer:

$$\overrightarrow{A_{A}}\,=\,{(0.5)\,\widehat{i}\,+\,(-0.98)\,\widehat{j}}\,\frac{m}{s^2}$$

$$\overrightarrow{A_{B}}\,=\,{\left(0.7\,cos\,50\right)\,\widehat{i}\,+\,\left(0.7\,sin\,50\right)\,\widehat{j}}\,\frac{m}{s^2}$$

$$\overrightarrow{A_{A/B}}\,=\,\overrightarrow{A_A}\,-\,\overrightarrow{A_B}$$

$$\overrightarrow{A_{A/B}}\,=\,{(0.05)\,\widehat{i}\,+\,(-1.52)\,\widehat{j}}\,\frac{m}{s^2}$$

$$A_{A/B}\,=\,\sqrt{\left(0.05\,\frac{m}{s^2}\right)^2\,+\,\left(-1.52\,\frac{m}{s^2}\right)^2}\,=\,1.52\,\frac{m}{s^2}$$

 

[andrevdh]

Its a privilege to help someone who enjoys his physics and gives me great pleasure.