- #1
Santilopez10
- 81
- 8
- Homework Statement
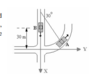
- Car A drives a curve of radius 60m with a constant velocity of 48 km/h. When A is at the given position, car B is at 30m away from the intersection and accelerating at 1.2 m/s^2 to the south. Calculate the lenght and direction of the acceleration that car B would measure of car A from its perspective at that instant.
- Relevant Equations
- Kinematic equations in polar and cartesian coordinates
I think my approach is quite wrong, still I gave it a shot:
First I know that ##v_A=13.3 m/s=r\omega=60\omega \rightarrow \omega=0.2 \frac{rad}{s}##
Then $$\vec a_A=-r\omega^2 e_r=-2.4 e_r$$
But ##e_r=\cos{\theta}i+\sin{\theta}j## and substituing the latter in the acceleration equation I have that ##\vec a_A= -2i-1.2j##
At last: $$\vec a_{A/B}=\vec a_A - \vec a_B$$
and this is were I stopped, hope you can help me. Thanks!
First I know that ##v_A=13.3 m/s=r\omega=60\omega \rightarrow \omega=0.2 \frac{rad}{s}##
Then $$\vec a_A=-r\omega^2 e_r=-2.4 e_r$$
But ##e_r=\cos{\theta}i+\sin{\theta}j## and substituing the latter in the acceleration equation I have that ##\vec a_A= -2i-1.2j##
At last: $$\vec a_{A/B}=\vec a_A - \vec a_B$$
and this is were I stopped, hope you can help me. Thanks!