- #1
A M
- 83
- 16
- TL;DR Summary
- I wanted to write a student article specially for those who don't have a background in nuclear physics. I've been suggested to share my basic understanding & ask if they're correct.
I would be grateful if anyone could explain where my mistakes are:
(Please note that diagrams are designed just to give a simple imagination of the article & make it more understandable; they do NOT correspond precise information.)
Exothermic process is a [nuclear] reaction in which energy is released, but for endothermic processes energy is needed. What does this released or needed energy come from?
Let's say we have the fusion shown in this picture:
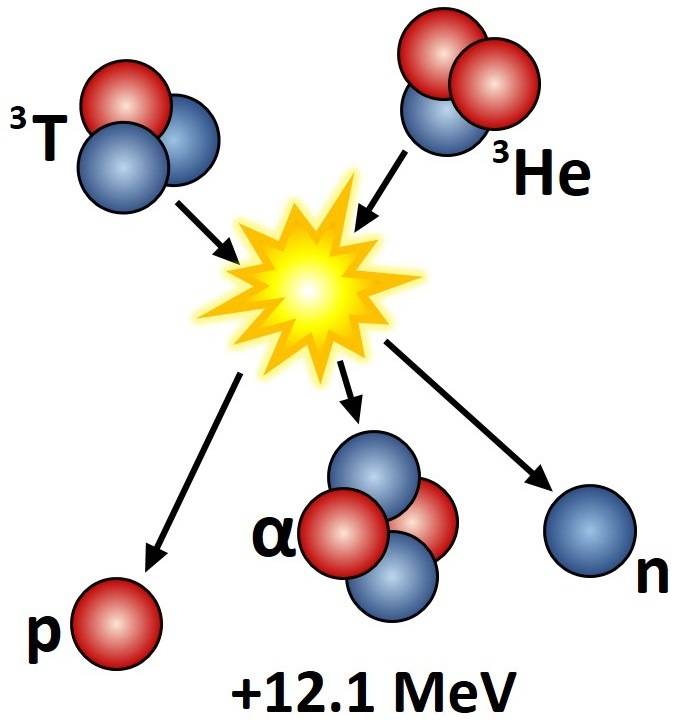
##m_h, m_t, m_α, m_p, m_n## - masses of helium-3, tritium, helium-4, free proton, and free neutron
##E## - released/utilized energy
The illustrated fusion is:
##m_h+m_t=m_α+m_n+m_p+E##
Now we can write:
##m_h+m_t-m_α-m_n-m_p=E##
##M_1-M_2=\Delta m=E##
Therefore, in all chemical and nuclear reactions, released/utilized energy corresponds the difference in initial and final masses (in relation with Einstein's equation).
According to the definition of mass defect & binding energy:
##m_h=2m_p+m_n-B_h##
##m_t=m_p+2m_n-B_t##
##m_α=2m_p+2m_n-B_α##
So, for the reaction we can also write:
##(2m_p+m_n-B_h)+(m_p+2m_n-B_t)=(2m_p+2m_n-B_α)+m_n+m_p+E##
By cancelling out all the rest masses of free nucleons we would have:
##-B_h-B_t=-B_α+E##
##B_α -B_h-B_t =E##
##B_2-B_1=\Delta B=E##
Now, we can conclude that for many nuclear reactions (except ε, β+, β-) the released/utilized energy comes from the difference between initial and final binding energies.
Energy released in some nuclear reactions is on the order of a million times greater than in chemical reactions; because [the difference in] nuclear binding energy is much larger than [the difference in] electron binding energy.
Now let's throw them into the mix!
##M_1## / ##M_2## - total mass of reactants/products
##B_1## / ##B_2## - total binding energy of reactants/products
##M_1-M_2=B_2-B_1=E~
\begin{cases}
\mathsf {If }~ E>0 ⇒ \mathsf {Exothermic } ⇒ \mathsf {Released~Energy} =E \\
\mathsf {If }~ E<0 ⇒ \mathsf {Endothermic } ⇒ \mathsf {Needed~Energy } =-E
\end{cases}##
####
That energy then is released as [electromagnetic or particle] radiation or kinetic energy of nuclei.
That energy (E>0) then is released as [electromagnetic or particle] radiation or kinetic energy of nuclei.
References:
https://www.physicsforums.com/posts/6216782/
Let's say we have the fusion shown in this picture:
##m_h, m_t, m_α, m_p, m_n## - masses of helium-3, tritium, helium-4, free proton, and free neutron
##E## - released/utilized energy
The illustrated fusion is:
##m_h+m_t=m_α+m_n+m_p+E##
Now we can write:
##m_h+m_t-m_α-m_n-m_p=E##
##M_1-M_2=\Delta m=E##
Therefore, in all chemical and nuclear reactions, released/utilized energy corresponds the difference in initial and final masses (in relation with Einstein's equation).
According to the definition of mass defect & binding energy:
##m_h=2m_p+m_n-B_h##
##m_t=m_p+2m_n-B_t##
##m_α=2m_p+2m_n-B_α##
So, for the reaction we can also write:
##(2m_p+m_n-B_h)+(m_p+2m_n-B_t)=(2m_p+2m_n-B_α)+m_n+m_p+E##
By cancelling out all the rest masses of free nucleons we would have:
##-B_h-B_t=-B_α+E##
##B_α -B_h-B_t =E##
##B_2-B_1=\Delta B=E##
Now, we can conclude that for many nuclear reactions (except ε, β+, β-) the released/utilized energy comes from the difference between initial and final binding energies.
Energy released in some nuclear reactions is on the order of a million times greater than in chemical reactions; because [the difference in] nuclear binding energy is much larger than [the difference in] electron binding energy.
Now let's throw them into the mix!
##M_1## / ##M_2## - total mass of reactants/products
##B_1## / ##B_2## - total binding energy of reactants/products
##M_1-M_2=B_2-B_1=E~
\begin{cases}
\mathsf {If }~ E>0 ⇒ \mathsf {Exothermic } ⇒ \mathsf {Released~Energy} =E \\
\mathsf {If }~ E<0 ⇒ \mathsf {Endothermic } ⇒ \mathsf {Needed~Energy } =-E
\end{cases}##
####
That energy then is released as [electromagnetic or particle] radiation or kinetic energy of nuclei.
That energy (E>0) then is released as [electromagnetic or particle] radiation or kinetic energy of nuclei.
References:
https://www.physicsforums.com/posts/6216782/
Last edited: