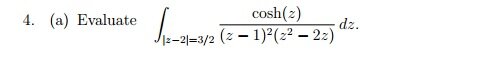nacho-man
- 166
- 0
Hi,
so first of all
I am not entirely confident with the terminology when it comes to classifying singularities.
Could someone give me an example of the different types, or explain what they mean? My confusion stems from the terms:
essential singularity, isolated singularity, removable singularity and pole of order m
I would prefer a non-mathematical jargonised definition, as these are readily available in my textbook, however I find them difficult to comprehend.
I know that $e^{\frac{1}{Z}}$ has an essential singularity at $z=0$
But I don't see what really distinguishes this and any other type of singularity. Except that you can't let z approach 0 and 'remove' it, i guess.
Whereas $\frac{1}{z-1}$ has a removable singularity at z=1. Is this also known as an isolated singularity?
$\frac{1}{z^2}$ does this have a pole of order 2 at z=0
WHat about $\sin{\frac{1}{z^2}}$ ?
Secondly, I have attached a residue question.
so far, I want to know if i am on the correct track.
$\cosh z = \frac{e^Z+e^{-Z}}{2}$
This is analytic everywhere, so we need not worry about this.
The poles are:
$z = 2$ is a removable pole? (i don't know if this is correct terminology)
$z=1$ is a pole of order 2
$z=0$ is a removable pole.
Am I on the right track so far?
I feel i might have missed something with the treatment $\cosh z$ part
Any help is very much appreciated, thanks!
so first of all
I am not entirely confident with the terminology when it comes to classifying singularities.
Could someone give me an example of the different types, or explain what they mean? My confusion stems from the terms:
essential singularity, isolated singularity, removable singularity and pole of order m
I would prefer a non-mathematical jargonised definition, as these are readily available in my textbook, however I find them difficult to comprehend.
I know that $e^{\frac{1}{Z}}$ has an essential singularity at $z=0$
But I don't see what really distinguishes this and any other type of singularity. Except that you can't let z approach 0 and 'remove' it, i guess.
Whereas $\frac{1}{z-1}$ has a removable singularity at z=1. Is this also known as an isolated singularity?
$\frac{1}{z^2}$ does this have a pole of order 2 at z=0
WHat about $\sin{\frac{1}{z^2}}$ ?
Secondly, I have attached a residue question.
so far, I want to know if i am on the correct track.
$\cosh z = \frac{e^Z+e^{-Z}}{2}$
This is analytic everywhere, so we need not worry about this.
The poles are:
$z = 2$ is a removable pole? (i don't know if this is correct terminology)
$z=1$ is a pole of order 2
$z=0$ is a removable pole.
Am I on the right track so far?
I feel i might have missed something with the treatment $\cosh z$ part
Any help is very much appreciated, thanks!
Attachments
Last edited: