mastermechanic
- 107
- 15
- Homework Statement
- Rigid body kinetics problem involving Impulse-Momentum application
- Relevant Equations
- G = m.v and H = m.v.r
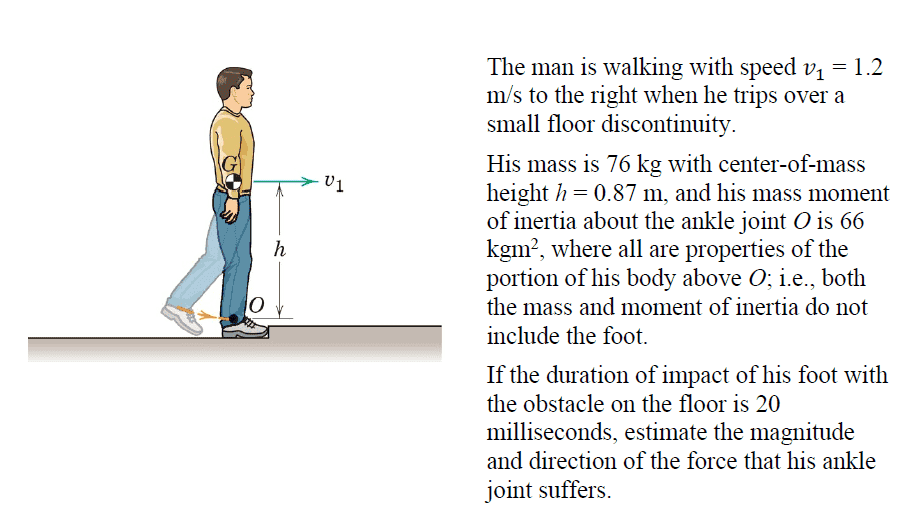
PROBLEM
Here from the conservation of angular momentum I found angular velocity just before impact,
$$ H_1 = 0 $$
$$ H_2 = I_0\omega + mV_0d $$
$$ H_2 = 66\omega + 76.(1.2).(0.87)$$
$$ H_1 = H_2 $$
$$ \omega = 1.202 rad/s $$
But I couldn't solve it to find joint force.
Thanks in advance,
Here from the conservation of angular momentum I found angular velocity just before impact,
$$ H_1 = 0 $$
$$ H_2 = I_0\omega + mV_0d $$
$$ H_2 = 66\omega + 76.(1.2).(0.87)$$
$$ H_1 = H_2 $$
$$ \omega = 1.202 rad/s $$
But I couldn't solve it to find joint force.
Thanks in advance,
Last edited: