Rock Climbing - American Death Triangle

[Obediah2]

This is the first time I've ever been to this forum, so I'm hoping this is an appropriate place to post this. It's been a good amount of time since my college level physics courses and this rock climbing phenomenon has me stumped. There is a rock climbing anchor arrangement called the "American Death Triangle" and it is a BAD way to make an anchor at the top of a rock. It's bad for a variety of reasons, but the most interesting is that it is a "force multiplier" due to it's geometry. There are plenty of "rules of thumb" that explain how the forces are multiplied with different angles at botton of the triangle, but I can't find (or make) a proof starting from basic FBD - vector addition - trig that will give me exact numbers as I change the angle. I'm hoping someone here can help.

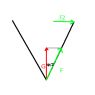
Dang I have no idea how to draw on here. Imagine you have one continuous piece of rope and two fixed points some horizontal distance apart. The rope fits loosely around the points so that the bottom of the loop is sagging. You then attach a weight to the bottom only and the resulting shape is an isosceles triangle with the base angles at the fixed points.

http://www.viswiki.com/en/American_death_triangle" is some more info.

I'm trying to calculate the forces that will be on the anchor points in terms of F (the force applied at the bottom) and the angle at the bottom (which will change depending on the distance between anchor points and the length of the loop)

Thanks

 

[cesiumfrog]

The force on the anchors must be directed almost horizontally (since tensions are in the direction of the ropes), therefore this force must be very large (since only the vertical component of it must balance an anchor's share of the weight loaded below); it certainly isn't half of the total weight (contrary to naive expectation).

It might be easiest to draw the FBD for the (massless & frictionless) rope triangle as a single point, exerting six equal forces (which must balance 2+1 applied forces), carefully noting the 3x2 directions from the geometry.

 

[0xDEADBEEF]

I would calculate it like this. G is the force of pull to counteract the weight:
F=G/ (2 \sin (\varphi /2))
There is a second force F2 on each hook that comes from the line tension between the hooks. It is the same F=F2
The angle between the two is
\gamma = 90^\circ -\varphi /2
From the parallelogram of forces you should get for the total force F3 on each hook:
F3=2 F \cos ( \gamma /2 )

 

[cesiumfrog]

http://en.wikipedia.org/wiki/American_death_triangle" is some more info.

Fixed that for you. Better to link to the http://en.wikipedia.org/wiki/American_death_triangle" wikipedia, that way you get the equations and not the advertising. By the way, this rock climbing error is a very interesting application (I'd not seen it before) of the physics of ropes with transverse forces, so thankyou.

I would calculate it like this[...] you should get for the total force F3 on each hook:
F3=2 F \cos ( \gamma /2 )

I think you need to go further to get the important result.

So for V-arrangement:
F_{anchor}=T=\frac W {2 cos \frac \theta 2} = 0.5 W + O(\theta^2)

But for the American death triangle:
F_{anchor}=2Tcos(45^\circ- \frac \theta 4)=\frac W {2 cos (45 ^\circ + \frac \theta 4)} \approx 0.707 W + O(\theta)

(in terms of the bottom angle. Note limiting behaviour as this approaches 180 degrees. Incidentally, the sling tension is the same in both cases.)

 

[Obediah2]

Thanks everyone - those equations are perfect. I was getting caught up for some reason on the feeling that I couldn't calculate the tension using only the y-direction ...I overlooked that using the angle automatically includes the effects of the horizontal portion. Interestingly enough, a logic breakdown that I remember from college.

Fixed that for you. Better to link to the original wikipedia, that way you get the equations and not the advertising. By the way, this rock climbing error is a very interesting application (I'd not seen it before) of the physics of ropes with transverse forces, so thankyou.

Thanks for the help and I'm glad you liked the application. It is so counter intuitive to me that it would be better to tie off to one bolt than two if the bottom angle is too big (from a strictly force based perspective anyway). That's the fun of physics I guess.