RicardoMP
- 48
- 2
Homework Statement
Hi! I'm trying to solve a simple problem of mechanics, but I'm getting the wrong results and I suppose I don't yet grasp the concept of instantaneous axis of rotation very well.
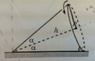
So, a cone (see attached picture) is rolling without slipping on a plane. Vp is point P linear velocity on the laboratory frame with its origin on the cone's apex. I must choose "z" as the vertical axis and, instantaneously, "x" along the line of contact.
I have to find the instantaneous angular velocity vector \omega.
Homework Equations
\omega = \Omega + \omega _s
\Omega = \frac{v_p}{hcos(\alpha)}
\omega _s = \frac{v_p}{R}
The Attempt at a Solution
My first thought was that there are 2 contributions for the angular velocity: \Omega pointing upwards and relates to the rotation of the cone around the vertical axis going through the origin and \omega _s which is the spin angular velocity of the cone. I simply decomposed the spin ang.vel in its x and z components and got
\omega = (\omega_s cos(\alpha))e_x+(\omega_s sin(\alpha) + \Omega)e_z
And I thought that was it.
The solution states that the angular velocity only has component along x: \omega = (\omega,0,0) and I'm failing to see how. Is the line of contact an instantaneous axis of rotation? And what does that mean for this problem?
Thank you in advance
Attachments
Last edited: