Priyanka88
- 13
- 4
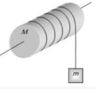
A mass m is tied to a string which is wrapped to a twig of a tree. How many minimum times should we wrap the string so that it doesn't fall?
Here is what i got...
1.There is friction between the twig (or fixed cylinder) and the string.
2. if the total friction between the string wrapped around in 1 circle around the cylinder it will be a piece of cake.
3. The thing is that i am unable to find that because the operating friction force at every point from the free body diagram will be different
Here is what i got...
1.There is friction between the twig (or fixed cylinder) and the string.
2. if the total friction between the string wrapped around in 1 circle around the cylinder it will be a piece of cake.
3. The thing is that i am unable to find that because the operating friction force at every point from the free body diagram will be different
Attachments
Last edited: