Rotational Motion / Torque Question

[PherricOxide]

Homework Statement

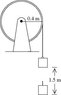
A wheel has a radius of 0.40 m and is mounted on frictionless bearings. A block is suspended from a rope that is wound on the wheel and attached to it. The wheel is released from rest and the block descends 1.5 m in 2.00 s while the wheel rotates clockwise. The tension in the rope during the descent of the block is 20 N.

Find the mass of the block.

Homework Equations

$$\theta$$ = (1/2)$$\alpha$$t^2 + $$\omega$$₀*t + $$\theta$$₀

$$\tau$$ = I$$\alpha$$

The Attempt at a Solution

Finding the angular acceleration,
-1.5m / 0.4m * 2pi = (1/2)$$\alpha$$*2²
$$\alpha$$ = -(1.5/0.4)pi

Converting that to the y acceleration of a point on the outside,
a_y = -1.5pi

From there, I tried to do T - mg = m*a_y and solve for mass,
-20N - m*9.8 = -m*1.5pi
m = -20/(-9.8-1.5pi)
m =~ 1.378

However, this isn't correct. The only choices are,
2.0 kg
2.2 kg
2.1 kg
1.9 kg
2.3 kg

And I think it has something to do with torque... I also tried to work through it with torque, but that didn't get me anywhere,
T = R*T = I*$$\alpha$$
-0.4*20 = I*-(1.5/0.4)pi
I = (0.4*20)/((1.5/0.4)pi)

 

[kuruman]

Although the question of the problem is not stated, I assume you are trying to find the hanging mass. The correct equation of motion for it is

T - mg = - ma_y (You left out the minus sign)

Forget the wheel. You know T and you know g. Can you find a_y if you are told that the mass starts from rest and descends 1.5 m in 2.0 s? If so, then you can find m.

 

[PherricOxide]

Yes, I'm trying to find the mass of the hanging object.

For something starting at rest at y=0,
y = (1/2)at^2
-1.5 = (1/2)*a*2^2
a = -0.75

From there,
T - mg = -ma_y
20 - m*9.8 = m*0.75
20 = m(0.75+9.8)
m = 20/(0.75+9.8)
m =~ 1.9kg.

However, this still isn't the right answer... It shows the correct answer as 2.2kg, I just can't figure out where it came from.

 

[tiny-tim]

Hi PherricOxide!

… a = -0.75

From there,
T - mg = -ma_y
20 - m*9.8 = m*0.75

You're confused about which way is up …

one of those minuses is wrong. ​

 

[PherricOxide]

20-9.8*m = m*(-0.75)

There we go, thanks guys. I'm still wondering why this was in the chapter with dynamics of rotational motion though.. I guess that's just a harder way to solve it.

 

[AakashR]

Here is the answer-

We can see that both the weight of the block and tension in the rope are constant. So, acceleration of the block is going to remain constant.

let's consider vertically downward direction as +Y. We have ΔY=1.5m and Δt=2.0s. Now, by using the formula ΔY=0.5a(Δt)^2, we can find "a" which is 0.75ms^-2.

In this problem the forces that are acting on the block are T, tension in the rope and weight of the object which we can consider to be mg.

ΣF=ma=mg-T where T is 20N.

Now by substituting the values into the equation and we'll get m=2.21kg i.e 2.2kg to 2s.f.

 

[tiny-tim]

Hi AakashR!

Please do not give complete answers.​