Rotational Physics - Bead on spinning ring

[AgentRedfield]

I think I'm not understanding some conceptual part of rotational kinematics because all the questions seem connected. I want to figure it out as best I can so please don't solve it but any hints in the right direction would be really appreciated, thanks!

The Question:
A stiff piece of wire is bent into a circle and mounted (vertically) to rotate as shown. A wooden bead with a hole through its center can slide frictionlessly on that wire. The radius of the wire hoop is 15.0 cm and it rotates steadily with a period of 0.450 s
.

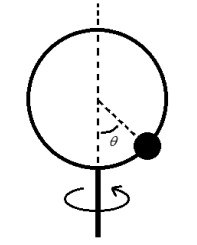
a) At what angle θ will the bead rotate, along with the hoop, without sliding (up or down)? Show that there are two possible angles (solutions) for this hoop size and rotational speed. Include a clear free body diagram of the bead as part of your solution.
b) At what period would the ball not leave the bottom position (θ =0)?
c) At what period would θ =90 degrees? What would that angular speed then be? Explain, in terms of forces on the bead, why one can’t spin the hoop fast enough for the bead to reach θ =90 degrees.
d) If the hoop were twice the radius, what would be the non-zero angle (at which the bead would rotate)?

Relevant Equations:
F_g=mg
a=mv²/r
v=wr
w=(2*pi)/T

Attempt at solving:

a) If the bead is at θ then there is a normal force directed towards the center of the circle and the force of gravity directed downward. Sum of forces in the 'y' gives Ncosθ-F_g=0 and in 'x' is Nsinθ=ma
I think the acceleration is rw² so lots of substitution gives θ=tan^-1 (rw² /g)
θ=71.47 degrees
This answer seems reasonable but I'm not sure if I skipped something. Also I don't know how to find the second angle.

b) I think F_g=N but if θ is zero it seems like acceleration would be zero so period would be zero which makes no sense.

c) Normal force would be zero and F_g=mv²/r
so g=rw² and w=2pi/T, after substitution I got:

w=8.08 rad/s²
T=0.777 s

I think I'm missing the conceptual part of c because my answer seems like normal numbers.

d) I imagine this would be solved the same as part a but the question seems to imply it would only have one angle it rotates at, what changed?

Thanks again for your time and help!

 

[TSny]

I think the acceleration is rw² so lots of substitution gives θ=tan^-1 (rw² /g)
θ=71.47 degrees

What is the meaning of r here?

 

[AgentRedfield]

What is the meaning of r here?

Is it not radius?

edit: Would it be r*sin(theta), where r is 0.15 m?

 

[TSny]

Is it not radius?

edit: Would it be r*sin(theta), where r is 0.15 m?

Note that the $r$ goes back to using $v^2/r$ for the acceleration. So, you just need to consider the meaning of $r$ as used in $v^2/r$. Then you can decide with confidence if $r = (.15 \rm{m}) \sin \theta$.

 

[AgentRedfield]

Since I'm saying acceleration is only in the x-direction then the $r$ should be $Rsinθ$ because that is the x-component of $r$.

My Work:
y:
$N \cos \theta = mg$
$N=\frac{mg}{\cos \theta}$
x:
$N \sin \theta = \frac{mv^2}{r} = \frac{mv^2}{R\sin \theta}$
$N = \frac{mv^2}{R}$
$\frac{mg}{\cos \theta} = \frac{mv^2}{R}$
$\cos \theta = \frac{gR}{(\frac{2 \Pi R}{T})^2}$

Answer:
$\theta = 70.42^{\circ}$

This is really close to my earlier answer. The logic of the steps seem right though. I'm also not sure how to get the second angle it would stay at.

Thanks for your help!

 

[TSny]

I believe your answer for $\theta$ is correct. I'm not quite sure of the interpretation of part (a) in regard to finding the second angle. Are negative values of $\theta$ allowed? Do they only want stationary positions of the bead that are stable with respect to small disturbances away from the stationary positions?