Rotational torque and kinematics of a rod

[ac7597]

Homework Statement

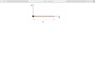
A long thin rod is made out of wood with a uniform density. It has a mass M=2.1 kg and a length L=1.2 meters. The rod is attached to a pivot point at its left end; it is free to rotate around the pivot, but, right now, Fred is holding it horizontal, as shown.

The pivot point sits at the origin of the coordinate system, with the x-axis running to the right and the y-axis pointing upward.

What is the moment of inertia of the rod around the pivot?
Where is the center of mass of this rod? Provide the coordinates in unit-vector notation.

Gravity acts on the rod as if it were pulling directly on the center of mass location. What is the magnitude of the gravitational torque around the pivot point?

Fred now releases the rod. It starts to swing down in response to the gravitational torque. After a short time, the rod has rotated by an angle β=20 degrees.

What is the position of the center of mass now?

What is the change in the gravitational potential energy of the rod, compared to its value when the rod was horizontal? Make sure you supply the appropriate sign.

What is the rotational kinetic energy of the rod at this moment?

What is the angular velocity of the rod at this moment?

Relevant Equations

torque= force * radius* sin(theta) = (moment of inertia) (angular acceleration)

moment of inertia = (1/3) (2.1kg) (1.2m)^2 = 1.0 kgm^2
center of mass= (0.6i, 0j)
magnitude of the gravitational torque=9.8m/s^2*2.1kg*0.6m= 12.34N*m

position of the new center of mass now :
x direction = cos(20)*0.6m=0.56m
y direction= -sin(20) * 0.6m = -0.2m

change in gravitational torque= -(9.8m/s^2*2.1kg*0.6m)sin(20)= -4.2N*m
rotational KE = (1/2) (moment of inertia) (angular velocity)^2
I don't confused on how to proceed further

 

[TSny]

change in gravitational torque= -(9.8m/s^2*2.1kg*0.6m)sin(20)= -4.2N*m

Is there a typo here? Did you mean to say "change in gravitational torque?"

rotational KE = (1/2) (moment of inertia) (angular velocity)^2
I don't confused on how to proceed further

Is there any relationship between the change in KE and the change in PE?

 

[ac7597]

They should be the same in magnitude because conversion of energy.
PE=mass*gravity*height = (2.1kg)(9.8ms/s^2) (-0.2m)= -4.1J

 

[TSny]

OK, total energy is conserved. Try to use that.

 

[ac7597]

thus KE=4.1J
since rotational KE = (1/2) (moment of inertia) (angular velocity)^2
4.1J = (1/2) (1kgm^2) (angular velocity)^2
angular velocity = 2.86 rad/s

 

[TSny]

I believe that's correct.