Russian Roulette probability distribution

[SpY]]

Hi. This isn't exactly like the previous thread and not a homework problem. I'd just like to check the validity of my solution. It concerns the relation between a discrete and continuous probability distribution.

The problem:
A player inserts a bullet into a 6-chamber revolver. He then spins the drum and points it to his head. If he lives, he re-spins the drum and tries again. Find the mean number of trials before he shoots himself.

Discrete solution
So this is clearly a discrete problem and statistically independent (re-spinning) so I'll start defining the discrete probability distribution for him dying in the n'th game.
P_D(n)={\frac{5}{6}}^{n-1}\frac{1}{6}

Finding the mean for the discrete case is easy -
\overline{n}= \sum_{n=1}^{\infty}n{\frac{5}{6}}^{n-1}\frac{1}{6}<br />
Let q=\frac{5}{6} and rewrite the argument of the sum as a partial derivative:
\frac{1}{6} \sum_{n=1}^{\infty}\frac{\partial }{\partial q}q^n
Which can be taken out of the sum (linear) and we use the formula for geometric series (q<1):

\frac{1}{6} \frac{\partial }{\partial q}\frac{q}{1-q}<br /> = \frac{1}{6} \frac{q}{(1-q)^2}

Then substituting q=5/6 we get the mean to be 6.Continuous solution
Though not technically allowed, define the probability density function for dying in the x'th game:
<br /> p(x)={\frac{5}{6}}^{x-1}\frac{1}{6}

Now to try this as a continuous problem through an integral:
\overline{x} =\int_{0}^{\infty}x \frac{1}{6} \big( \frac{5}{6} \big)^{x-1} dx
= \frac{1}{6} \frac{6}{5} \int_{0}^{\infty} x (\frac{5}{6})^x dx

Through IBP (or wolframalpha) where u=x and dv= dx q^x and q=5/6
= \frac{1}{5} \big( \frac{x\cdot q^x}{ln(q)} - \frac{q^x}{(ln(q))^2} \big) \right|_0^\infty

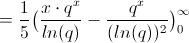
For these limits I'm taking a leap of faith, particularly the first term. As a product of a linear (x) and exponential (q^x), to zero they both go to zero - but to infinity, one goes to infinity and the other to zero. The limit of a product is the product of the limits only when they are not infinite (I'm sure). Otherwise I'm saying ∞*0 = 0 ...

By some numerics, putting in x=1000 the result is to the order 10^-77. The graph of p(x) also tends to zero as x goes to infinity. So assuming the limits for this term go to zero, I then have

= \frac{1}{5\cdot(ln(q))^2}

Substituting q I get the mean to be 6.02... sufficiently close to the 6 - as I got previously. Not sure of the significance of the error though...My question is what I did with an integral mathematically valid? One of those cases where getting the correct answer doesn't necessarily mean your method is ok..

Also, can we use a continuous distribution (integral) as an approximation for a discrete distribution (riemann sum)?

 

[mathman]

My question is what I did with an integral mathematically valid? One of those cases where getting the correct answer doesn't necessarily mean your method is ok..

Also, can we use a continuous distribution (integral) as an approximation for a discrete distribution (riemann sum)?

The answer to the first question is yes for q < 1, q^x goes to 0 a lot faster than x becoming infinite. The easiest way to see it is use L'hopital's rule on x/q^-x.

Using the integral as an approximation is valid.