S4.13.t.71 angles of triangle PQR

[karush]

$\tiny{s4.13.t.71}$
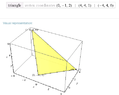
$\textsf{For the given points
$P(0,-1,2), Q(4,4,1), R(-4,4,6)$}$
$\textsf{Find the approximate measurements
of the angles of $\triangle$ PQR. }$

$\textit{Ok, presume its get vectors first
then use Dot Product...}$

$\textit{First find vectors $\vec{PQ},\vec{QR},$ and $\vec{RP}$}$
\begin{align*}\displaystyle
\vec{PQ}&=\langle 0-4,-1-4, 2-1 \rangle =\langle -4,-5,1 \rangle\\
\vec{QR}&=\langle 4+4,-4-4, 2-1 \rangle =\langle 8,0,-5 \rangle\\
\vec{RP}&=\langle-4-0,4+1,6-2 \rangle=\langle -4,0,4 \rangle\\
\end{align*}
$\textit{Calculate the dot product and magnitudes of first two vectors.}$\begin{align*}\displaystyle
\vec{PQ}\cdot\vec{QR}&=(-4)(8)+(-5)(0)+(1)(-5)=-37\\
|\vec{PQ}|&=\sqrt{(-4)^2+(-5)^2+(1)^2}=\sqrt{41}\\
|\vec{QR}|&=\sqrt{(8)^2+(0)^2+(-5)^2}=\sqrt{99}\\
\end{align*}
$\textit{now apply angle formula}$
\begin{align*}\displaystyle
\theta&=\cos^{-1}\left[\frac{\vec{PQ}\cdot\vec{QR}}{|\vec{PQ}||\vec{QR}|}\right]\\
&=\cos^{-1}\left[\frac{-37}{|\sqrt{41}||\sqrt{99}}\right]\\
&=\cos^{-1}(-0.5807)=2.1905 radians
\end{align*}

I think so far...

 

[Greg]

Your approach is correct. I haven't checked the arithmetic. :p

 

[Greg]

Two of the dot products are negative suggesting two of the angles are $>90^\circ$. (Wondering)

 

[karush]

Two of the dot products are negative suggesting two of the angles are $>90^\circ$. (Wondering)

Sorry spent an hour trying to find the errors but still
so before I take the arccos would this be correct
I found about 5 oops

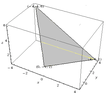
$\textsf{ For the given points
P(0,-1,2), Q(4,4,1), R(-4,4,6) }\\$

$\textsf{Find the approximate measurements
of the angles of $\triangle$ PQR. }\\$

$\textit{First find vectors $\vec{PQ},\vec{QR},$ and $\vec{RP}$}$
\begin{align*}\displaystyle
\vec{PQ}&=\langle (0-4),(-1-4),(2-1) \rangle =\langle -4,-5,1 \rangle\\
\vec{QR}&=\langle (4+4),(4-4),(1-6) \rangle =\langle 8,0,-5 \rangle\\
\vec{RP}&=\langle (-4-0),(4+1),(6-2) \rangle=\langle -4,5,4 \rangle\\
\end{align*}
$\textit{Calculate the dot product and magnitudes of first two vectors.}$
\begin{align*}\displaystyle
\vec{PQ}\cdot\vec{QR}&=(-4)(8)+(-5)(0)+(1)(-5)=-37\\
\vec{QR}\cdot\vec{RP}&=(8)(-4)+(0)(5)+(-5)(4)=-52\\
\vec{RP}\cdot\vec{PQ}&=(-4)(-4)+(-5)(5)+(4)(1)=-5\\
|\vec{PQ}|&=\sqrt{(-4)^2+(-5)^2+(1)^2}=\sqrt{42}\\
|\vec{QR}|&=\sqrt{(8)^2+(0)^2+(-5)^2}=\sqrt{89}\\
|\vec{RP}|&=\sqrt{(-4)^2+(5)^2+(4)^2}=\sqrt{57}\\
\end{align*}

View attachment 7087
W|A answer
0.753 radians | 1.468 radians | 0.921 radians
interior angle sum | 180° = π rad≈3.142 rad)

 

[I like Serena]

I have a couple of observations:

1. When subtracting 2 vectors we have that $\vec{PQ}=\vec{OQ}-\vec{OP}$.
   That is, a vector is the endpoint minus the starting point.
   It appears that this has been reversed.
2. The dot product is that: $\vec{PQ}\cdot\vec{PR} = PQ\cdot PR\cdot \cos\angle P$.
   And $\vec{PR}=-\vec{RP}$, meaning we have to be careful with our signs. (Thinking)

 

[karush]

I have a couple of observations:

1. When subtracting 2 vectors we have that $\vec{PQ}=\vec{OQ}-\vec{OP}$.
   That is, a vector is the endpoint minus the starting point.
   It appears that this has been reversed.
2. The dot product is that: $\vec{PQ}\cdot\vec{PR} = PQ\cdot PR\cdot \cos\angle P$.
   And $\vec{PR}=-\vec{RP}$, meaning we have to be careful with our signs. (Thinking)

OK here is the redo...

$\textit{Calculate the dot product and magnitudes of first two vectors.}$
\begin{align*}\displaystyle
\vec{PQ}\cdot\vec{QR}&=(-4)(8)+(-5)(0)+(1)(-5)=37\\
\vec{QR}\cdot\vec{RP}&=(8)(-4)+(0)(5)+(-5)(4)=52\\
\vec{RP}\cdot\vec{PQ}&=(-4)(-4)+(-5)(5)+(4)(1)=5\\
|\vec{PQ}|&=\sqrt{(-4)^2+(-5)^2+(1)^2}=\sqrt{42}\\
|\vec{QR}|&=\sqrt{(8)^2+(0)^2+(-5)^2}=\sqrt{89}\\
|\vec{RP}|&=\sqrt{(-4)^2+(5)^2+(4)^2}=\sqrt{57}\\
\end{align*}
$\textit{Apply angle formula}$
\begin{align*}\displaystyle
{\angle PQR}
&=\cos^{-1}\left[\frac{\vec{PQ}\cdot\vec{QR}}{|\vec{PQ}||\vec{QR}|}\right]
=\cos^{-1}\left[\frac{37}{|\sqrt{42}||\sqrt{89}|}\right]
=0.921 \textit{ rad}\\
{\angle QRP}
&=\cos^{-1}\left[\frac{\vec{QR}\cdot\vec{RP}}{|\vec{QR}||\vec{RP}|}\right]
=\cos^{-1}\left[\frac{52}{|\sqrt{89}||\sqrt{57}|}\right]
=0.753 \textit{ rad}\\
{\angle RPQ}
&=\cos^{-1}\left[\frac{\vec{RP}\cdot\vec{PR}}{|\vec{RP}||\vec{PR}|}\right]
=\cos^{-1}\left[\frac{5}{|\sqrt{57}||\sqrt{42}|}\right]
=1.468 \textit{ rad}
\end{align*}

$\textsf{triangle A(0,-1,2), B(4,4,1), C(-4,4,6) }\\$
$\textsf{ 0.921 radians \\ 0.753 radians \\ 1.468 radians }\\$
$\textsf{interior angle sum $180°= π= 3.142$}$

View attachment 7109