Screw dislocation displacement discontinouty

[Paul Chen]

Consider a screw dislocation,

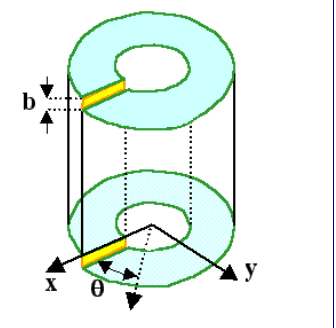
The displacement field is given by

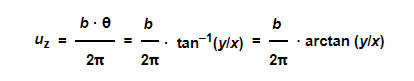
And the strain field is derived by

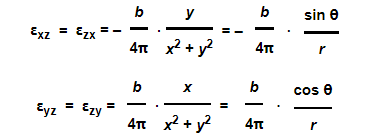
My question is that the displacement seems discontinuous across the dislocation surface (y=0, i.e., displacement jump from 0 to b), so why it is still differentiable on the surface and why the strain is continuous across the dislocation surface?

 

[hutchphd]

This is a continuum model and the arctangent is not discontinuous (look it up) .

 

[Paul Chen]

This is a continuum model and the arctangent is not discontinuous (look it up) .

Thanks for your reply. Yes, this is a continuum model and the stress should be continuous (except at the dislocation line). But if you look at the displacement field, it is indeed discontinuous across the dislocation surface, where the displacement suddenly jump from 0 to b). Please see the figure below. My question is that how can a discontinouse displacement field produce a continouse strain field?

The acrtangent function (arctan(x)) is a multivalued function, i.e., it hasmultiple values (0, 2π, 4π...) when x=0, that is why the displacement field is discontinouse.

Figure source: Verschueren, J., Gurrutxaga-Lerma, B., Balint, D. S., Dini, D., & Sutton, A. P. (2017). The injection of a screw dislocation into a crystal: Atomistics vs. continuum elastodynamics. Journal of the Mechanics and Physics of Solids, 98, 366-389.

 

[hutchphd]

But in the wake of the dislocation there is slip and the strain field is defined in terms of the final equilibrium coordinates. Clearly at the center (r=0) point of the dislocation things are not well defined but the "step" is cooked into the formalism for the rest as shown

 

[Paul Chen]

But in the wake of the dislocation there is slip and the strain field is defined in terms of the final equilibrium coordinates. Clearly at the center (r=0) point of the dislocation things are not well defined but the "step" is cooked into the formalism for the rest as shown

I find in some textbook that the displacement 'step change' across the dislocation surface is plastic deformation, so the actual elastic displacement field is continuous at the surface and the total displacement field (discontinuous) is the sum of the elastic-displacement (continues) and the plastic-displacement (slip b). The strain and stress we calculated using the equation are elastic, there also exists another plastic component.

Rf: Dislocations in solids. Vol. 1. The elastic theory edited by F. R. N. Nabarro, pp42-44.