Math Amateur
Gold Member
MHB
- 3,920
- 48
I am revising the Isomorphism Theorems for Groups in order to better understand the Isomorphism Theorems for Modules.
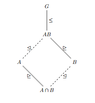
I need some help in understanding Dummit and Foote's proof of the Second Isomorphism Theorems for Groups (Diamond Isomorphism Theorem ? why Diamond ?).
The relevant text from D&F is as follows:
View attachment 3270
In the proof above we read:
"Proof: By Corollary 15, $$AB$$ is a subgroup of $$G$$.
Since $$A \leq N_G (B)$$ by assumption and $$B \leq N_G (B)$$ trivially ...
... it follows that $$AB \leq N_G (B)$$ i.e. $$B$$ is a normal subgroup of the subgroup $$AB$$ ... ... ... "
Can someone please explain to me why $$AB \leq N_G (B)$$ means that $$B$$ is a normal subgroup of the subgroup $$AB$$?
Peter
I need some help in understanding Dummit and Foote's proof of the Second Isomorphism Theorems for Groups (Diamond Isomorphism Theorem ? why Diamond ?).
The relevant text from D&F is as follows:
View attachment 3270
In the proof above we read:
"Proof: By Corollary 15, $$AB$$ is a subgroup of $$G$$.
Since $$A \leq N_G (B)$$ by assumption and $$B \leq N_G (B)$$ trivially ...
... it follows that $$AB \leq N_G (B)$$ i.e. $$B$$ is a normal subgroup of the subgroup $$AB$$ ... ... ... "
Can someone please explain to me why $$AB \leq N_G (B)$$ means that $$B$$ is a normal subgroup of the subgroup $$AB$$?
Peter