Ole Forsell
- 10
- 0
Hello.
I am currently working with a beam with the following cross-section:
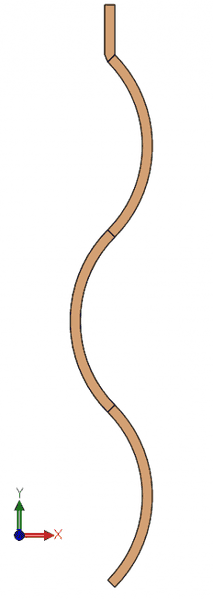
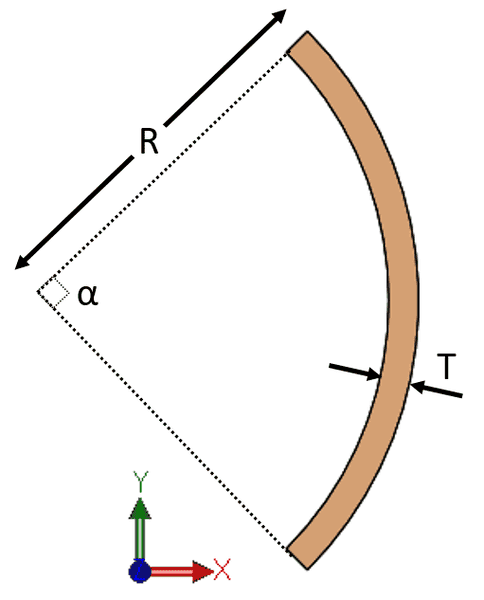
It consist of three bended sections with the following parameters, alpha = 90 degrees, Thickness = 4 mm, Radius = 50.59 mm.
The top section consist of a small triangle and a rectangle. the triangle have a width = 4 mm and height = 2.81 mm. The rectangle have width = 4 mm and height = 19.60 mm.
The area of the profile is given by the following equation, and should be approximately 1000 mm2:
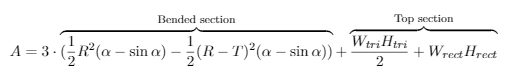
I need to find the deflection of this beam, and thereby the second moment of inertia. I have already found this to be 4273323.41 mm4 in Section Properties in Solidworks, but this need to be substantiated by hand calculations. Does anybody know how to calculate the second moment of inertia for such a geometry?Ole
I am currently working with a beam with the following cross-section:
It consist of three bended sections with the following parameters, alpha = 90 degrees, Thickness = 4 mm, Radius = 50.59 mm.
The top section consist of a small triangle and a rectangle. the triangle have a width = 4 mm and height = 2.81 mm. The rectangle have width = 4 mm and height = 19.60 mm.
The area of the profile is given by the following equation, and should be approximately 1000 mm2:
I need to find the deflection of this beam, and thereby the second moment of inertia. I have already found this to be 4273323.41 mm4 in Section Properties in Solidworks, but this need to be substantiated by hand calculations. Does anybody know how to calculate the second moment of inertia for such a geometry?Ole
Last edited: