Second order Sigma Delta modulator

[solanojedi]

Hi everybody,
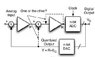
I'm reading about sigma delta adc, the base theory. I've read about the first order modulator and now the second order, but I have a problem (maybe stupid) with a phrase of my book (Data Converters by F.Maloberti), when he describe the 'passage' from first order to second order. He says: "Better performances and features are secured by using two integrators around the loop thus forming a second-order modulator as shown in the conceptual scheme of Fig. 6.11 (a). Since the use of two integrators in a feedback loop can
cause instability, it is necessary to dump one of the two integrators by using one of the two options represented by the dotted lines of Fig. 6.11 (a)." (Fig. 6.11 (a) is attached) Why two integrators in the loop can cause instability? I can't see why... Thank you very much!

 

[Okefenokee]

Let's say we took out the dotted lines. Let's also say that we are going to ignore any effect that the ADC/DAQ will have. In that case, we have a simple feedback system with the following relationships in the Laplace domain:

y(s) is the Laplace transform of the output.

x(s) is the Laplace transform of the input.

\frac{1}{s^2} is the Laplace transform of double integration.

The equation of the feeback is system it this:

y(s) = \frac{1}{s^2} \left( x(s) - y(s) \right)

Rearranging we will get:

y(s) = \frac{\frac{1}{s^2}}{1 + \frac{1}{s^2}} x(s)

y(s) = \frac{1}{s^2 + 1} x(s)

The polynomial of the denominator decides the stability (s^2 + 1). To be stable, the roots in the Laplace domain must have a negative real component. This system has roots 0-i,0+i. They are on the imaginary axis which means that just about any input will cause this system to oscillate.

 

[solanojedi]

Thanks for your answer!

The problem is that, if we analyze the system with the Laplace (or Z-transform), we can see that also in the first order modulator we have a 1/1+s in the transfer function, so also the first order must be instable. I think the instability should be analyzed without linear methods, because it is a non linear system. So, there is a book or a paper where I can find a discussion about the stability of this architecture of second order sigma modulator? [i.e, a first order modulator with two integrators in series instead of one]
Thank you!

 

[Okefenokee]

the root of \frac{1}{1 + s} is -1

It's stable.

 

[solanojedi]

Ooops, you're right..! :)
Thank you!

 

[Okefenokee]

No problem, good luck with your studies.