Self-inductance of LC circuit given rate of capacitor discharge.

[zenterix]

Homework Statement

Initially, the capacitor in a series LC circuit is charged. A switch is closed, allowing the capacitor to discharge. After a time $t_1$, the energy stored in the capacitor is one fourth of its initial value.

Relevant Equations

Calculate the value of the self-inductance $L$ in terms of $t_1$ and $C$.

We seem to have the following circuit

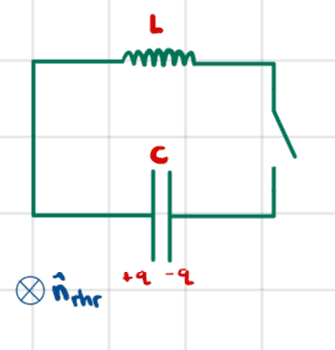
and the differential equation $\ddot{q}+\omega^2q=0$ where $\omega=\frac{1}{\sqrt{LC}}$.

The solution is

$$q(t)=A\cos{(\omega t+\phi)}$$

Since $I(t)=-\dot{q}(t)$ we have

$$I(t)=-\dot{q}(t)=A\omega\sin{(\omega t+\phi)}$$

At $t=0$ we have

$$q(0)=A\cos{\phi}$$

$$I(0)=A\omega\sin{\phi}=0\implies \phi=0$$

Thus,

$$q(0)=A$$

There is no battery in the circuit and no resistance in the wires. The total energy in inductor and capacitor is constant.

The energy in the capacitor is

$$U_E(t)=\frac{q(t)^2}{2C}=\frac{A^2}{2C}\cos^2{(\omega t)}$$

and the energy in the inductor is

$$U_B(t)=\frac{LI^2(t)}{2}=\frac{L}{2}A^2\omega^2\sin^2{(\omega t)}$$

$$=\frac{A^2}{2C}\sin^2{(\omega t)}$$

I am stuck trying to find an expression for $L$ in terms of $t_1$.

 

[Orodruin]

You have not used the requirement that the energy in the capacitor should be a fourth of its initial value. What does this requirement tell you?

 

[hutchphd]

Given the "no loss" (zero resistace) clause in the question, this circuit will oscillate asy ou described . There will be cyclic repeated times when this energy division occurs and the question is therefore incomplete. Prof gets a Fail.

 

[zenterix]

Here is what I did to solve the problem.

The energy in the capacitor at time $t_1$ is

$$U_E(t_1)=\frac{A^2}{2C}\cos^2{(\omega t_1)}=\frac{1}{4}U_E(0)=\frac{A^2}{8C}$$

$$\implies \cos^2{(\omega t_1)}=\frac{1}{4}$$

$$\cos{(\omega t_1)}=\pm\frac{1}{2}$$

This equation is satisfied at four different values of $\omega t_1\in [0,2\pi)$.

Since $\omega=\frac{1}{\sqrt{LC}}$ is a fixed number, then we have four different times at which the energy in the capacitor is a fourth of the initial (maximal) value.

Let's consider one of four instances.

$$\omega t_1=\frac{\pi}{3}$$

and after subbing in for $\omega$ and solving for $L$ we get

$$L=\frac{9t_1^2}{C\pi^2}$$

 

[hutchphd]

there you go. Note thisw will also be a problem (multiple roots) for small but finite R where the solution is a decaying oscillation. The result will no longer be exactly cyclic, but may yield several posible roots before the energy is dissipated in the resister. I could make a nastier similar problem out of this idea..

 

[zenterix]

@hutchphd

In this hypothetical problem you mention there is a resistor (so that we have an series RLC circuit) and so we end up with damping.

What do you mean the result "may yield several possible roots before the energy is dissipated in the resistor"?

 

[Orodruin]

What do you mean the result "may yield several possible roots before the energy is dissipated in the resistor"?

The charge/current oscillates with a decaying amplitude. If you specify that charge should be some fraction of the initial charge, this may occur at several different times.