evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
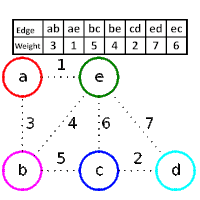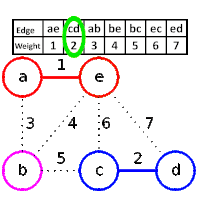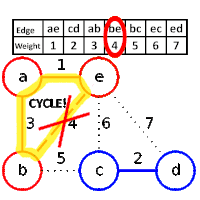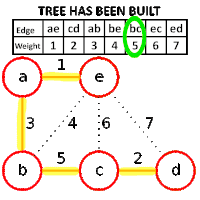
Could you explain me some sentences,that are related to the following algorithm?
Could you explain me some sentences,that are related to the following algorithm?
Code:
Template algorithm(G)
A<-∅
while A isn't a connected tree
we define an edge (u,v),that is secure for A
A<-A U {(u,v)}
return A- Let $G=(V,E)$ be an undirected connected graph with weight function $w:E \to \mathbb{R}$.Let $A \subseteq E$,that is contained in a minimum spanning tree for the graph $G$ and let $(S, V \setminus S)$ any intersection of $G$,that respects $A$.Let,also, $(u,v)$ a light edge,crossing the intersection $(S, V \setminus S)$.Then,the edge $(u,v)$ is secure for $A$.
$$$$ - A minimum spanning tree isn't unique.
$$$$ - The Template Algorithm is implemented at most $|V|-1$ times.
$$$$
Does this sentence maybe stand,because of the fact that $G$ is connected,so $|E|=|V|-1$,and if during the implementation,cycles aren't created,the "while" loop is implemented so many times as the number of edges,so $|V|-1$ times? (Thinking)
$$$$ - Let $G_A=(V,A)$.Then, $G_A$ is a forest and each of its connected components , is a tree.
Why is $G_A$ a forest and not a connected tree,although the condition of the algorithm is:
Code:while A isn't a connected tree
? (Thinking)
$$$$ - Any secure edge $(u,v)$ for $A$ connects different components of $A$.
Last edited: