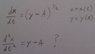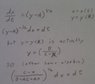Separating variables within square root expressions

[timsea81]

Please see attached. This is a general question for a more complex thermo problem, but it fits this form. Are there any tricks to getting expressions out of square roots in solving DEs?

y=y(x)
x=x(t)

I want to get y by itself so I can integrate with respect to x, but it is trapped in a square root expression. My guess of squaring both sides and "squaring" the dx/dt term by making it a second derivative doesn't seem right, but it's all I can think up. Does anyone have any suggestions?

 

[hunt_mat]

So you have a coupled system:
$$\begin{array}{rcl}<br /> \frac{dx}{dt} & = & \sqrt{y-A} \\<br /> \frac{d^{2}x}{dt^{2}} & = & y-A<br /> \end{array}$$
So this gives the ODE
$$\frac{d^{2}x}{dt^{2}}=\left(\frac{dx}{dt}\right)^{2}$$
Let $v=dx/dt$, so:
$$\frac{dv}{dt}=v^{2}$$
Can you take it from here?

 

[timsea81]

Looking back on it I guess my original post was misleading.

The second derivative statement wasn't a given criteria, that was my first guess at how to solve the problem (squaring both sides but for the left hand side the squaring process involves taking it to its second derivative). That doesn't work, I tried it out with some real equations and thought about it some more and concluded it is pure nonsense.

I think I got it though. I know what y=y(x) is so I can plug it into the left hand side and get a complicated expression where x is the only variable and I can integrate. It's ugly, but it works.

 

[hunt_mat]

The definition of y would have been helpful, but you did the right thing.