Solve the Partial differential equation ##U_{xy}=0##

[chwala]

TL;DR Summary

I am going through these notes; i want to check that i am gettting it right...

Solve the pde;

$U_{xy}=0$

This is part of the notes;

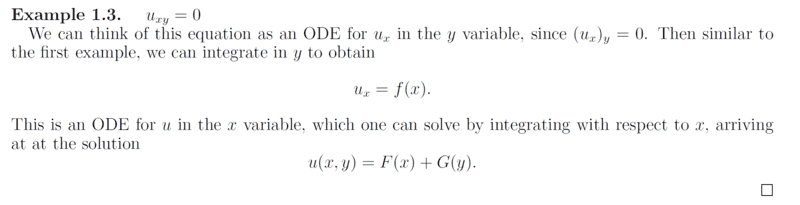
My own way of thought;

Given;

$U_{xy}=0$

then considering $U_x$ as on ode in the $y$ variable; we integrate both sides with respect to $y$ i.e

$\dfrac{du}{dx} \int \dfrac{1}{dy} dy=\int 0 dy$

this is the part i need insight...the original problem involves partial derivatives but in this case when we integrate with respect to $y$ we are integrating with respect to $dy$ and not $∂y$ ...correct?

$U_x= 0 + k$, where $k$ is a constant in terms of $x$ therefore,

$U_x= f(x)$, an arbitrary function of $x$... which is an ode for $u$ in the $x$ variable. On integrating again with respect to $x$ we get,$U(x,y) = F(x) + k$, where $k$ is a constant in terms of $y$ therefore,

$U(x,y) = F(x) + H(y)$cheers!

 

[anuttarasammyak]

I interpret you as follows.
$$\frac{\partial^2 U(x,y)}{\partial x \partial y}=0$$
Integration by y with x=const. or by x with y=const.
$$\frac{\partial U}{\partial x }=f(x)$$
$$\frac{\partial U}{\partial y }=g(y)$$
Thus
$$dU=f(x)dx+g(y)dy$$
$$U(x,y)=F(x)+G(y)$$

 

[chwala]

I interpret you as follows.
$$\frac{\partial^2 U(x,y)}{\partial x \partial y}=0$$
Integration by y with x=const. or by x with y=const.
$$\frac{\partial U}{\partial x }=f(x)$$
$$\frac{\partial U}{\partial y }=g(y)$$
Thus
$$dU=f(x)dx+g(y)dy$$
$$U(x,y)=F(x)+G(y)$$

Is there another way bro? ...they call it method of characteristic ...need to read on this...

 

[Mark44]

Given;
$U_{xy}=0$

then considering $U_x$ as on ode in the $y$ variable; we integrate both sides with respect to $y$ i.e

$\dfrac{du}{dx} \int \dfrac{1}{dy} dy=\int 0 dy$

The above doesn't make any sense to me. Clearly the last integral would be 0 + a constant.

this is the part i need insight...the original problem involves partial derivatives but in this case when we integrate with respect to $y$ we are integrating with respect to $dy$ and not $∂y$ ...correct?

The expression $dy$ serves only to indicate the variable with respect to which integration is taking place. You are integrating with respect to y, not dy, and definitely not with respect to ∂y.