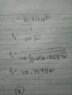Butterfly41398
- 8
- 0
Poster has been reminded to post schoolwork in the Homework Help forums
Summary:: About resonant frequencies
A series RLC circuit with R = 250 ohms and L = 0.6 H results in a leading phase angle of 60° at a frequency of 40 Hz. At what frequency will the circuit resonate?
Answer is 81.2 Hz but i got a different answer. May someone please correct me.
A series RLC circuit with R = 250 ohms and L = 0.6 H results in a leading phase angle of 60° at a frequency of 40 Hz. At what frequency will the circuit resonate?
Answer is 81.2 Hz but i got a different answer. May someone please correct me.