Set of points on the complex plane

[cbarker1]

Dear Everybody, I am wanting to check the solution to this question:

Sketch the set of points determined by the given conditions:
a.) $\left| z-1+i \right|=1$
b.)$\left| z+i \right|\le3$
c.)$\left| z-4i \right|\ge4$

work:
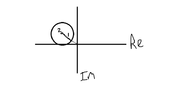
I know (a.) is a circle with radius 1 and its center at (-1,1) on the complex plane see in figure 1.
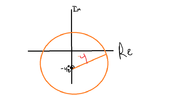
I know (b.) is a circle with radius 3 and its center at (0,1) on the complex plane see in figure 2.
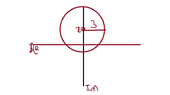
I know (c.) is a circle (?) with radius 4 with its center (0,-4) on the complex plane see in figure 3.

Thanks
Cbarker1

 

[HOI]

Almost. But "=", "$$\le$$", and "$$\ge$$" are not the same! In general, |z- a| is the distance from complex number z to complex number a. Yes, the set of points, z, in the complex plane, such that |z- 1+ i|= |z- (1- i)|= 1 is the circle with center at 1- i, (1, -1), and radius 1. Similarly, |z+ i|= 3 is the circle with center at i, (0, 1), and radius 3. But your problem has $$\le$$ rather than =. In addition to the circle where the distance is equal to 3, this set contains also the interior of the circle, the "disk" with center at i and radius 3.

Likewise, (c) is the circle with center 4i, (0, 4), and all points outside that circle.

 

[math771]

Hello Cbarker1,

Your solutions for (a.) and (b.) are correct. However, for (c.), the set of points determined by the condition $\left| z-4i \right|\ge4$ is not a circle, but rather the area outside of the circle with radius 4 and center at (0,-4). This is because the inequality $\left| z-4i \right|\ge4$ means that the distance between the point z and the point (0,-4) is greater than or equal to 4. Therefore, any point that falls outside of the circle with radius 4 and center at (0,-4) satisfies this condition.

I hope this helps clarify your solution for (c.). Keep up the good work!