Setup for Spherical Astronomy Problem

[Kelli Van Brunt]

Homework Statement

A full moon occurred on June 19, 2008 at 00h 30m West Indonesian Time (local civil time for western part of Indonesia with reference to geographic longitude of 105° E). Calculate the extreme values of duration of the Moon above the horizon for observers at Bosscha Observatory (longitude: 107º 35' 00″.0 E, latitude: 6º 49' 00″.0 S, Elevation: 1300.0 m). Time zone = UT +7h 00m.

Relevant Equations

None; this is a conceptual question

My apologies for not detailing my attempts at a solution; I'm not sure how to to digitally illustrate or describe the various setups I attempted before looking at the solution to this problem. I am also ONLY asking about the setup, though I included the full question for context.
The solution to this problem has the following setup:

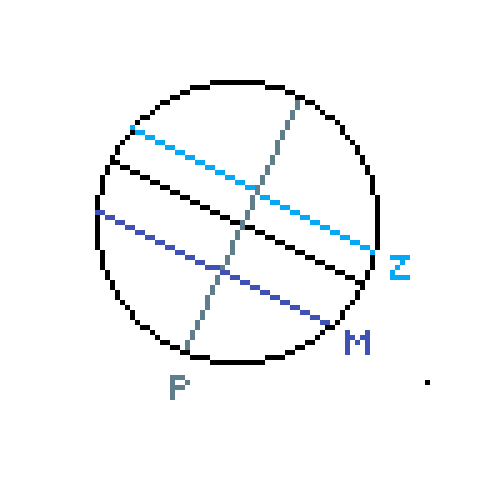
Where Z = zenith, P = south celestial pole, and M = moon (I assume represented by the path of the little blue spheres). SP is the latitude of the observing site and PM is 90º - declination of Moon. My main question is, why is P above the horizon/NESW plane when the latitude of the observing site is positive? Shouldn't an observer in the north not be able to "see" the south celestial pole? I drew a diagram of the situation in the equatorial plane below and am wondering why this is not the correct setup. The horizontal analogy to this would, I assume, be the above diagram but with the moon's path, celestial equator, and celestial south pole shifted clockwise so that M is to the right of the zenith and P is below the horizon. I apologize for my very bad graphic design skills. Can anyone clarify this for me?

EDIT: Sorry for posting this twice - that was an accident.

 

[collinsmark]

My main question is, why is P above the horizon/NESW plane when the latitude of the observing site is positive? Shouldn't an observer in the north not be able to "see" the south celestial pole?

Bosscha Observatory is south of the equator. Although the latitude was given as an unsigned value, you know that it's south of the equator by the "S" at the end of ... latitude: 6º 49' 00″.0 S.

 

[Kelli Van Brunt]

Bosscha Observatory is south of the equator. Although the latitude was given as an unsigned value, you know that it's south of the equator by the "S" at the end of ... latitude: 6º 49' 00″.0 S.

I can't believe I missed that, thank you so much. That cleared up everything.