Short Exact Sequences & Direct Sums .... Bland, Proposition 3.2.7

[Math Amateur]

I am reading Paul E. Bland's book "Rings and Their Modules" ...

Currently I am focused on Section 3.2 Exact Sequences in $\text{Mod}_R$ ... ...

I need some help in order to fully understand the proof of Proposition 3.2.7 ...

Proposition 3.2.7 and its proof read as follows:

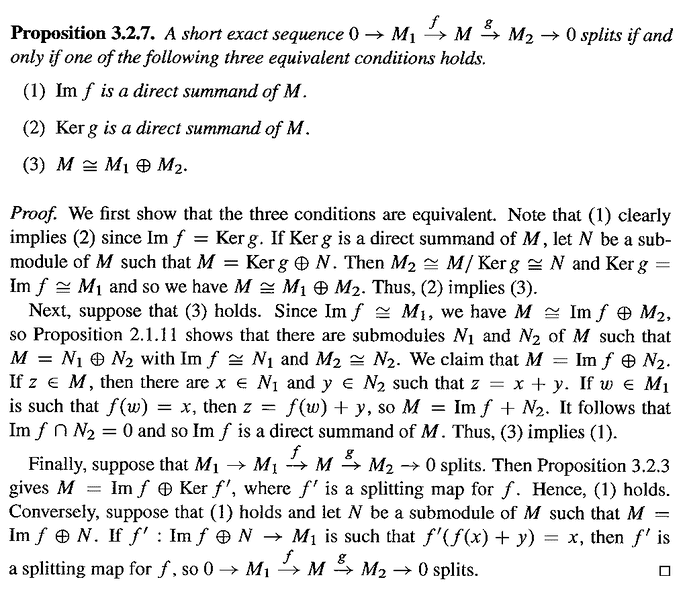
In the above proof we read the following:

"... ... Then $M_2 \cong M/ \text{ Ker } g \cong N$ and $\text{ Ker } g = \text{ I am } f \cong M_1$ ... ...My questions regarding the above are as follows:Question 1I understand that $M_2 \cong M/ \text{ Ker } g$ by the First Isomorphism Theorem for Modules ... ... but why is $M_2 \cong M/ \text{ Ker } g \cong N$ ... ... ?Question 2Why, exactly, is $\text{ Ker } g = \text{ I am } f \cong M_1$ ... ... ?

Help will be much appreciated ...

Peter

 

[andrewkirk]

For (1) consider the map $h:N\to M_2$ such that $h(n)=g(n)$. This is linear, since it is a restriction of the map $g$ which is linear. We just need to show that it is mono and epi, for it to be an isomorphism. Have a go and see what happens. You'll be using the fact that $g$ is epi and that $M=\mathrm{Ker\ }g\oplus N$.

For (2), the fact that $\mathrm{Ker}\ g=\mathrm{Im}\ f$ is given by the definition of Exact Sequence, which is that the image of one linking map is the kernel of the next.
The fact that $\mathrm{Im}\ f\cong M_1$ follows from the fact that $f$ is linear and mono (both given facts) and by definition of Image it is epi on its own image, so $f$ is an isomorphism between its domain $M_1$ and its image. Indeed, more generally for every monomorphism the domain is isomorphic to the image.

Strictly speaking, specification of a function involves specifying the range as well as the map, so $f$ with its range altered from $M$ to $\mathrm{Im\ }f$ is technically a different function from $f$. But such niceties are brushed aside where they are not important to the argument.

 

[Math Amateur]

For (1) consider the map $h:N\to M_2$ such that $h(n)=g(n)$. This is linear, since it is a restriction of the map $g$ which is linear. We just need to show that it is mono and epi, for it to be an isomorphism. Have a go and see what happens. You'll be using the fact that $g$ is epi and that $M=\mathrm{Ker\ }g\oplus N$.

For (2), the fact that $\mathrm{Ker}\ g=\mathrm{Im}\ f$ is given by the definition of Exact Sequence, which is that the image of one linking map is the kernel of the next.
The fact that $\mathrm{Im}\ f\cong M_1$ follows from the fact that $f$ is linear and mono (both given facts) and by definition of Image it is epi on its own image, so $f$ is an isomorphism between its domain $M_1$ and its image. Indeed, more generally for every monomorphism the domain is isomorphic to the image.

Strictly speaking, specification of a function involves specifying the range as well as the map, so $f$ with its range altered from $M$ to $\mathrm{Im\ }f$ is technically a different function from $f$. But such niceties are brushed aside where they are not important to the argument.

Thanks for the help, Andrew ...

You write:

"... ... For (1) consider the map $h:N\to M_2$ such that $h(n)=g(n)$. This is linear, since it is a restriction of the map $g$ which is linear. We just need to show that it is mono and epi, for it to be an isomorphism. Have a go and see what happens. You'll be using the fact that $g$ is epi and that $M=\mathrm{Ker\ }g\oplus N$. ... ... "

Well ... first show that h is surjective ... where $h \ : \ N \longrightarrow M_2$ where $h(n) = g(n)$ ... ...

Let $m \in M$ ... then there exists $l \in \text{ Ker } g$ and $n \in N$ such that $m = l + n$ ...

So then ... $g(m) = g(l + n) = g(l) + g(n) = 0 + g(n) = g(n) = h(n)$

Therefore since $g$ is surjective we have that $h$ is surjective ...Hmmm ... not sure at all about that "proof"

Can you help ... ?
To show that $h$ is injective we need to show that ...

$h(n_1) = h(n_2) \Longrightarrow n_1 = n_2$ ...

But ... how do we proceed ... ?

Again ... can you help ...

Peter

 

[andrewkirk]

To show surjectivity of $h$ it makes sense to start by using the surjectivity of $g$. Given $y\in M_2$ there must exist $m\in M$ such that $y=g(x)$. Now you can tack on your reasoning above to find $n\in N$ such that $h(n)=g(n)=y=g(m)$.

For mono, start by assuming $h(n_1)=h(n_2)$ where $n_1,n_2\in N$. Use the fact that $h$ is a restriction of $g$, and then the linearity of $g$, to show that $n_1-n_2\in\mathrm{Ker}\ g$. Since $n_1-n_2$ is also in $N$, what then must its value be?

 

[Math Amateur]

Thanks Andrew ...

Now ... try again ...

To show that h is surjective ...

Let $y \in M_2$ ...

Then $\exists \ m \in M$ such that $y = g(m)$ since $g$ is surjective ...

But ... $g(m) = g(l + n) = g(l) + g(n) = 0 + g(n) = g(n) = h(n)$ ...

So ... $y = h(n)$ for some $n \in N$ ... that is $h$ is surjective ...Is that correct?
To show that h is injective ...$h(n_1) = h(n_2)$

$\Longrightarrow g(n_1) = g(n_2)$

$\Longrightarrow g(n_1) - g(n_2) = 0$

$\Longrightarrow g(n_1 - n_2) = 0$

$\Longrightarrow n_1 - n_2 \in \text{ Ker } g$

... BUT ... $n_1 - n_2 \in N$ and we have $N \cap \text{ Ker } g = 0$

Therefore $n_1 - n_2 = 0 \Longrightarrow n_1 = n_2$ ...

... and so ... $h$ is injective ...Is that correct ... ?Thanks again for all your help ...

Peter

 

[andrewkirk]

Yes that's good. The surjectivity proof is sound, but I would be inclined to replace the first 'But' by something like

"because $M=\mathrm{Ker}\ g\oplus N$ there must exist $l\in\mathrm{Ker}\ g$ and $n\in N$ such that $m=l+n$"

to justify the steps we take there.

The proof of injectivity is excellent.

 

[steenis]

Q1: Verify $M/ker g \cong N$ given that $M = ker g \oplus N$. This is answered in the other forum, I copy it here.
By the Third Isomorphism Theorem and because $kerg \cap N = 0$ we have

$N \cong \frac{N}{ker g \cap N} \cong \frac{kerg + N}{ker g} = \frac{M}{ker g}$

Q2: verify $im f \cong M_1$
Define $f_1:M_1 \to I am f$ by $x \mapsto fx$, it is easy to show that $f_1$ is a monomorpism and an epimorphism

 

[Math Amateur]

Thanks for all your help Andrew ...

Thanks Steenis... just reflecting on your post now ...

Peter

 

[mathwonk]

(edit): I believe this "theorem" is not true as stated, since I think it is possible for a module M to be isomorphic to the direct sum of M1 and M2 without the sequence being split. (see counterexample below in post #13.)

 

[fresh_42]

this "theorem" is not true as stated, since it is quite possible for a module M to be isomorphic to the direct sum of M1 and M2 without the sequence being split. this suggests to me the advisability of possibly changing books.

Can you elaborate this? E.g. my book about homological algebra (proof inclusive) I found:

The author calls such a sequence exact direct, which is a bit more telling, if one the equivalent conditions hold:
$$
0 \longrightarrow M_1 \stackrel{f}{\longrightarrow} M \stackrel{g}{\longrightarrow} M_2 \longrightarrow 0 \Longleftrightarrow M_1 \stackrel{f}{\rightarrowtail} M \stackrel{g}{\twoheadrightarrow} M_2
$$

1. $\exists \,h: M \longrightarrow M_1 \oplus M_2\, : \,M\cong_h M_1 \oplus M_2$
2. $\exists \,g': M_2 \longrightarrow M \, : \, g \circ g' = \operatorname{id}_{M_2}$
3. $\exists \,f': M \longrightarrow M_1 \, : \, f' \circ f = \operatorname{id}_{M_1}$

So how should an example in such a commutative environment (ring multiplication, module addition) look like, such that the sequence doesn't split?

 

[mathwonk]

well to be honest i was just recalling "well known" facts, so i need to do some research to back it up. but intuitively the distinction is between whether some isomorpism exists between M and that direct sum, and whether the specific maps given in the sequence led to such a direct sum decomposition. but i think your book also suffers from the same flaw. let me search and see if i am just wrong. of course if you have vetted the proof then i will have trouble.

well maybe i am being careless but here in wikipedia is the version i support, namely note that the third equivalent condition says explicitly that the direct sum decomposition must use the given injection in the exact sequence as the one in the direct sum decomposition:

https://en.wikipedia.org/wiki/Splitting_lemmai still need to find you a counterexample, but this strengthens my confidence that they exist.
...so far the "counterexample" i have found is not commutative, so does not qualify, i.e. the quaternion units wrt the cyclic groups of orders 2,4. so i am not as confident again.

 

[fresh_42]

In general a split only leads to a semi-direct sum, but all semi-direct sums are direct given commutativity, because the inner automorphism which establishes the product operation breaks down to the identity. That's what I have in mind without looking for proofs in detail. So one has to be careful with groups and algebras.

 

[mathwonk]

whew! here it is.

http://www.math.uconn.edu/~kconrad/blurbs/linmultialg/splittingmodules.pdf

let f inject Z into Z by multipliucation by 2. then map this also into Z + (Z/2)^infinity, by sending n to (2n,0), with quotient (Z/2)^infinity+1 ≈ (Z/2)^infinity.

then this is apparently a counterexample. i.e. 0-->Z-->Z + (Z/2)^infinity --> (Z/2)^infinity -->0.

i.e. the first map, although injective, has no left inverse. so although the center module is isomorphic to the direct sum of the two extreme modules, the image of the first injection is not a direct summand.let me know if I have screwed this up. but i have considered this fact as very well known for 40-50 years.

 

[fresh_42]

whew! here it is.

http://www.math.uconn.edu/~kconrad/blurbs/linmultialg/splittingmodules.pdf

let f inject Z into Z by multipliucation by 2. then map this also into Z + (Z/2)^infinity, by sending n to (2n,0), with quotient (Z/2)^infinity+1 ≈ (Z/2)^infinity.

then this is apparently a counterexample. i.e. 0-->Z-->Z + (Z/2)^infinity --> (Z/2)^infinity -->0.

i.e. the first map, although injective, has no left inverse.let me know if I have screwed this up. but i have considered this fact as very well known for 40-50 years.

Thanks. It'll take me a while (for other reasons) but I will certainly have a look. It's a nice puzzle to find the actual flaw in either of them. But the homological proof is so easy that I find it hard to believe it could be wrong. But a quick look at your example is pretty convincing.

 

[mathwonk]

the error in bland's proof is in line -3,-2 of the second paragraph where he assumes that because Im(f) ≈ N1, that the actual given map f is an isomorphism, and hence he assumes there is a point w such that f(w) = x. in my example the map f does not map onto any such element x. this tells me this author is not an expert. i suggest reading books by artin, van der waerden, eilenberg - maclane, northcott, Lang,... of course anyone can make a mistake, but this is really well known basic information in homological algebra. almost the next sentence after defining split sequences used to be to remind you that this stronger statement is not true.

I want to readily admit there are also multiple errors in my books and notes, probably more blatant than this. But the authors I recommend tend not to make as many as most of us. On the other hand if this book is easy to understand, we should just forgive the occasional error. But in general, one learns more from the great authorities.

By the way fresh42, your book's statement seems also clearly false. perhaps he copied Bland's "proof"?

 

[fresh_42]

I'm not quite familiar with your notation (Z/2)^infty. Do you mean $\mathbb{N}$ copies of $\mathbb{Z}_2$?

Anyway, I've found the next book with the same statement in an exercise (Hilton, Stammbach, GTM 4, p.22, ex.3.7). So I assume there's something missing which I don't see yet. It's definitely too late here. My suspicion is that in $2\mathbb{Z} \rightarrowtail \mathbb{Z} \twoheadrightarrow \mathbb{Z}_2$ the integers aren't a direct product of groups, but of $\mathbb{Z}-$modules: $n = (2n, n \operatorname{mod}2)$.

 

[mathwonk]

yes i meant a direct sum of a countable number of copies of Z/2. that example you give is not split of course, since Z is not isomorphic to Z/2 + 2Z.

since peter hilton is an expert i assume you mean they have the correct statement. \\...
i just searched hilton and found their statement is indeed correct, but it is more precise than the false one in your quote (#1 in post 10), i.e. they assume the isomorphism involves the given map in the sequence, not some arbitrary map. in your book's statement #1, the isomorphic map h has no relation to the maps in the sequence, which is not sufficient.

Apparently Bland does not have a phd in mathematics, but has one in "curriculum and instruction". Still he knows a lot of algebra.

 

[fresh_42]

But isn't $g'(\bar{1})=1\; , \;g'(\bar{0})=0$ a split? With $g \, : \,\mathbb{Z} \longrightarrow \mathbb{Z}_2$ defined by modulo, don't we have $g\circ g' = \operatorname{id}_{\mathbb{Z}_2}$ and thus a direct sum of $\mathbb{Z}-$modules, just not Abelian groups? Sorry, if this was a stupid question, I'm a bit tired. I have to search for the truth, because three sources (Hilton-Stammbach, Brunner, Bland) all tell the same thing, and it should be wrong?

 

[mathwonk]

did you read my last post? hilton stambach do not say what you quote. Z modules and abelian groups are exactly the same thing. what are you asking? if your map g' is a map from Z/2 to Z, then notice any such map is identically zero, since it must be additive. i.e. since 1bar + 1bar = 0bar = 2.1bar, then 1bar must go to an element whose sum with itself is zero, and zero is the only such element. so you cannot define g' : Z/2-->Z taking 1bar to 1. this is not a Z module map, and (equivalently) not an abelian group map. so this is indeed confusing, but hilton-stammbach are correct and bland is not. i have not seen brunner. do you have a reference? what is brunner's full name?

 

[fresh_42]

did you read my last post? hilton stambach do not say what you quote. Z modules and abelian groups are exactly the same thing. what are you asking? if your map g' is a map from Z/2 to Z, then notice any such map is identically zero, since it must be additive. i.e. since 1bar + 1bar = 0bar = 2.1bar, then 1bar must go to an element whose sum with itself is zero, and zero is the only such element. so you cannot define g' : Z/2-->Z taking 1bar to 1. this is not a Z module map, and (equivalently) not an abelian group map. so this is indeed confusing, but hilton-stammbach are correct and bland is not. i have not seen brunner. do you have a reference? what is brunner's full name?

Yeah, right, I told you I'm tired and so haven't checked the homomorphism property of $g'$, sorry. His full name is Götz Brunner. His name won't tell you much, as he was a professor on a minor German university. The book is from the early '70s and just a short paperback on homological algebra, but the statement is basically the same as in Hilton's exercise, only without the $\operatorname{Hom}$ functor which he treats separately. I've seen your post but will have to read it tomorrow later. I couldn't see, yet, the discrepancies in the formulations, as the statement I quoted, which I translated from his book, is complete, except of the commutativity of a 6 module diagram (the outer connected by the identity), which therefore also involve the given mappings, the splits being defined on the isomorphic copy $M$ of $M_1 \oplus M_2$.

 

[andrewkirk]

he assumes there is a point w such that f(w) = x. in my example the map f does not map onto any such element x.

This looks right. When I read those lines of the proof I had the same reaction: what is the justification for assuming that a $w$ exists in $M_1$ such that $f(w)=x$? Indeed, the author starts the sentence with 'If', but then seems to forget about that conditional and just assume that it is so.

I could not follow the Example 1.4 in the linked paper by Conrad, because he uses an overbar notation (eg $\bar{y_0}$) that I do not recognise, together with terminology that I do not recognise (" 'reduces' the first component modulo $a$" and "shifts the other components over one position"). But, given the identified flaw in Bland's proof attempt, the notion that there could be a short exact sequence in which $M\cong M_1\oplus M_2$ but the map $f$ does not split because $M$ cannot be written as an internal direct sum $\mathrm{Im}\ f\oplus N_2$ seems plausible.

EDIT: Have now seen the post below. There is a good presentation of the counter-example in the top answer in the second link in Steenis's post. It's pretty easy to follow, up to the point at which it makes the claim "$\beta\circ s$ strictly decreases the order of $x$" - the truth of which is unfortunately not obvious to me. However, since the example looks the same as the one in Example 1.4 of Conrad (mathwonk's link), maybe using the stackexchange answer to understand the construction and then switching back to Conrad for the final demonstration that the sequence does not split would be a good strategy.

 

[steenis]

Yes, mathwonk is right. I have posted this error on "StackExchange Mathematics" a few years ago. See the threads:

https://math.stackexchange.com/questions/1884126/proposition-3-2-7-of-bland-on-short-exact-sequences

https://math.stackexchange.com/questions/1082283/example-of-a-non-splitting-exact-sequence-0-→-m-→-m-oplus-n-→-n-→-0

-

 

[mathwonk]

I have given Conrad's counterexample in post #13. where my notation (Z/2)^infinity means the direct sum of a countable number of copies of (Z/2), but I see the discussion linked by steenis in stackexchange is much more thorough and clear.

By the way, just perusing Bland's book, almost at the very beginning, on p. 7, he attributes a paper actually written by Emil Artin in 1927, to the son, Michael Artin, who was born in 1934. I was alerted to this because he uses the old term "hypercomplex systems" which are now called "algebras", as noted already in the 1940 edition of van der waerden.

 

[mathwonk]

fresh, omitting the part of the definition of "exact-direct" on brunner's page 105, that says the isomorphism with the direct sum makes the 6 term diagram commute, unfortunately is what makes the statement false. that commutativity is what guarantees the splitting, since as you say it links the direct sum maps with the original maps in the sequence. So now I believe Hilton-Stammbach and Brunner, have it correctly stated, but Bland does not.

 

[steenis]

See also

https://www.physicsforums.com/threads/split-exact-sequences-bland-proposition-3-2-7.881174/

posted Aug 6, 2016.

 

[mathwonk]

omyword, I'm losing my memory and reliving the same events, from less than 2 years ago. arggh!