Split Exact Sequences .... Bland, Proposition 3.2.7

[Math Amateur]

I need help to resolve an apparent contradiction between part of a Proposition proved by Paul Bland in his book "Rings and Their Modules" and an Example provided by Joseph Rotman in his book "An Introduction to Homological Algebra" (Second Edition).

One element of Bland's Proposition 3.2.7 is the assertion (and proof) that

$M \cong M_1 \oplus M_2$ ... ...

$\Longrightarrow$

... the short exact sequence

$0 \to M_1 \stackrel{f}{\to} M \stackrel{g}{\to} M_2 \to 0$

is splitHowever ... ...

Rotman in Example 2.29 (page 54) constructs a sequence

$0 \to A \stackrel{i'}{\to} A \oplus M \stackrel{p'}{\to} M \to 0$

which is not split ... ...

Thus Rotman appears to construct a counterexample to Bland's Theorem ...

BUT ...

how can this be ... ... ?

Can someone please resolve this issue ... ?

Help will be very much appreciated ... ...

PeterBland's Proposition 3.2.7 reads as follows:

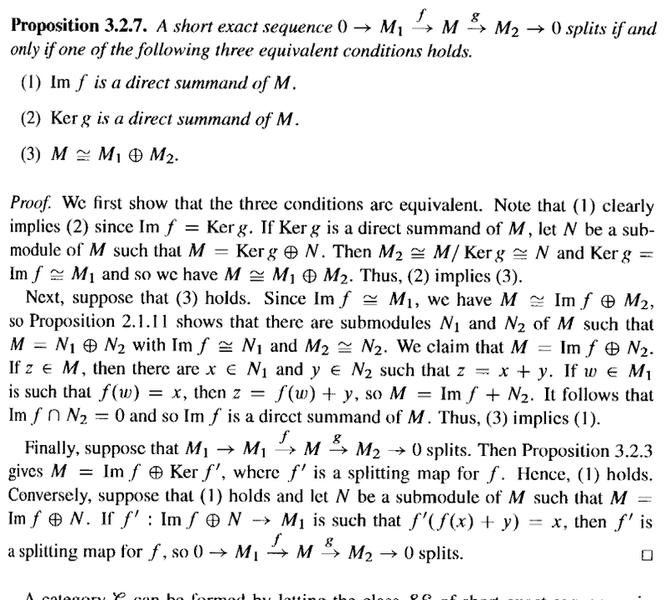
Rotman's Example 2.29 reads as follows:

To give readers the necessary Definitions and Propositions on exact sequences in Bland I am providing the following relevant text from Bland ... ...

 

[micromass]

The sequence in Rotman does not satisfy (1) and (2) frmo Bland.

 

[fresh_42]

I think your confusion is based on Rotman's notation $0 → S → S \oplus T → T → 0$.
That isn't the case in his example, because $S \oplus T = A \oplus A = ℤ_2 \oplus ℤ_2 \ncong ℤ_4 = B$ (as abelian groups).

In the module case as of Bland's Proposition 3.2.7 you have a natural embedding $m_1 \mapsto (m_1,0) = m_1 +0$ and a natural projection $m = m_1 + m_2 = (m_1,m_2) \mapsto m_2$ which almost splits by looking at it.

This isn't the case with the groups anymore, because Rotman maps the generator $b$ of $B=ℤ_4$ which is of order $4$ onto $a$, the generator of $A = ℤ_2$ which is of order $2$.

It is true that $ℤ_2 \overset{\iota}\rightarrowtail ℤ_4 \overset{\pi}\twoheadrightarrow ℤ_2$ defined by $\iota(a)=2b$ and $\pi(b)=a$ is a short exact sequence.
[Assume that it splits. Then there is a group homomorphism $\sigma : ℤ_2 → ℤ_4$ such that $\pi \sigma = id_{ℤ_2}$.
Now we have $a=\pi \sigma (a) = \pi (nb) = na$ for some $n$. But this only is true in $ℤ_2$ for $n=1$, i.e. $\sigma(a) = 1 \cdot b$. But this implies $1 = \sigma(1) = \sigma(2a) = \sigma(a) + \sigma(a) = b +b = 2b \neq 1$. Thus the sequence cannot split.]

Things change if we consider $ℤ_2 \times ℤ_2$ instead of $ℤ_4$.
For better distinction we may write $A = ℤ_2 = <a \, | \, a^2 = 1 >$ as above (only multiplicative) and $C = ℤ_2 \times ℤ_2 = ℤ_2 \oplus ℤ_2 \cong \{(1),(12),(34),(12)(34)\}$ as group of transpositions (permutations of order $2$).

Now we can define $ℤ_2 \overset{\iota}\rightarrowtail ℤ_2 \times ℤ_2 \overset{\pi}\twoheadrightarrow ℤ_2$ by $\iota(a)=(12)$ and $\pi(12)=a \, , \, \pi(34)=1$.

This sequence $A = ℤ_2 \overset{\iota}\rightarrowtail C = ℤ_2 \times ℤ_2 \cong A \oplus A \overset{\pi}\twoheadrightarrow ℤ_2 = A$ splits (with $\sigma(a) =(12)$) and is the corresponding situation to Bland's Proposition 3.2.7.

 

[Math Amateur]

I think your confusion is based on Rotman's notation $0 → S → S \oplus T → T → 0$.
That isn't the case in his example, because $S \oplus T = A \oplus A = ℤ_2 \oplus ℤ_2 \ncong ℤ_4 = B$ (as abelian groups).

In the module case as of Bland's Proposition 3.2.7 you have a natural embedding $m_1 \mapsto (m_1,0) = m_1 +0$ and a natural projection $m = m_1 + m_2 = (m_1,m_2) \mapsto m_2$ which almost splits by looking at it.

This isn't the case with the groups anymore, because Rotman maps the generator $b$ of $B=ℤ_4$ which is of order $4$ onto $a$, the generator of $A = ℤ_2$ which is of order $2$.

It is true that $ℤ_2 \overset{\iota}\rightarrowtail ℤ_4 \overset{\pi}\twoheadrightarrow ℤ_2$ defined by $\iota(a)=2b$ and $\pi(b)=a$ is a short exact sequence.
[Assume that it splits. Then there is a group homomorphism $\sigma : ℤ_2 → ℤ_4$ such that $\pi \sigma = id_{ℤ_2}$.
Now we have $a=\pi \sigma (a) = \pi (nb) = na$ for some $n$. But this only is true in $ℤ_2$ for $n=1$, i.e. $\sigma(a) = 1 \cdot b$. But this implies $1 = \sigma(1) = \sigma(2a) = \sigma(a) + \sigma(a) = b +b = 2b \neq 1$. Thus the sequence cannot split.]

Things change if we consider $ℤ_2 \times ℤ_2$ instead of $ℤ_4$.
For better distinction we may write $A = ℤ_2 = <a \, | \, a^2 = 1 >$ as above (only multiplicative) and $C = ℤ_2 \times ℤ_2 = ℤ_2 \oplus ℤ_2 \cong \{(1),(12),(34),(12)(34)\}$ as group of transpositions (permutations of order $2$).

Now we can define $ℤ_2 \overset{\iota}\rightarrowtail ℤ_2 \times ℤ_2 \overset{\pi}\twoheadrightarrow ℤ_2$ by $\iota(a)=(12)$ and $\pi(12)=a \, , \, \pi(34)=1$.

This sequence $A = ℤ_2 \overset{\iota}\rightarrowtail C = ℤ_2 \times ℤ_2 \cong A \oplus A \overset{\pi}\twoheadrightarrow ℤ_2 = A$ splits (with $\sigma(a) =(12)$) and is the corresponding situation to Bland's Proposition 3.2.7.

Micromass, fresh_42,

Thanks for the help ...

fresh_42, you are so right when you write:

" ... ... I think your confusion is based on Rotman's notation $0 → S → S \oplus T → T → 0$... ... "

Just working through the details of your post ...

Thanks again ...

Peter

 

[fresh_42]

Just working through the details of your post ...

I've made a little mistake. In order for the last sequence to be exact, it has to be $\iota(a) = (34)$, the other part of the direct product.

 

[mathwonk]

without reading the proofs, i think the problem may be that prop. 3.27 seems false unless part 3 is made more precise to include the map giving the isomorphism. to be sure i would have to read Bland's argument. but micromass's remark, and Rotman's example, if correct, seems to already imply that property 3) does not imply either 1) or 2).

 

[fresh_42]

If we have $M \cong_\varphi M_1 \oplus M_2$ (cond. 3), then $M_1$ and $M_2$ are per definition of $M$ direct factors of $M$.
Given any short exact sequence $M_1 \overset{f}\hookrightarrow M_1 \oplus M_2 \overset{g}\twoheadrightarrow M_2$ we therefore have up to isomorphism $im \, f = f(M_1) = \ker g$ as a direct factor of $M$ proving (cond. 1) and (cond. 2). In addition $M / \ker g =(M_1 \oplus M_2) / M_1 \cong M_2$ as well is a direct factor and the split homomorphism $\sigma$ of $M_2$ in $M$ is then the embedding and vice versa.
Having (1) ⇔ (2) and to say the sequence is short exact is somehow tautological.

My thoughts are circling now because it's difficult to distinguish between assumption and conclusion in the sense that it's not clear (to me) whether the sequence is also given or only the fact that it splits. Given (cond. 3) both is clearly true, i.e. embedding and projection define a short exact sequence that splits.

However, the essential part is the following:

A short exact sequence $A \overset{f}\rightarrowtail C \overset{g}\twoheadrightarrow B$ always defines a subobject $f(A) \subseteq C$ and an isomorphism (induced by $g$) $C / I am \, f = C / f(A) = C / \ker g \cong B$.
The clue here is (Prop. 3.2.7. evtl. following ones), that $B$ can be seen as a subobject of $C$ if and only if the sequence splits, making $C$ a direct product / sum.

Thus $\mathbb{Z_4}$ is an example for a case where the sequence doesn't split, because $\mathbb{Z_4} \ncong \mathbb{Z_2} \times \mathbb{Z_2}$. Another example would be $\mathbb{Z_6}$ versus $\mathcal{Sym}_3$ .

 

[micromass]

without reading the proofs, i think the problem may be that prop. 3.27 seems false unless part 3 is made more precise to include the map giving the isomorphism. to be sure i would have to read Bland's argument. but micromass's remark, and Rotman's example, if correct, seems to already imply that property 3) does not imply either 1) or 2).

That's right. Bland's proof is incorrect. Specifically, in his proof of (3) => (1), he hasn't justified why a $w$ needs to exists for which $f(w) = x$. So that is an incorrect step.

If you want your sequence to be split, then you need your entire short exact sequence to be isomorphic to the direct product sequence. Just having that $M$ is isomorphic to a direct sequence is not good enough.

 

[mathwonk]

thank you micromass for spelling this out. I believe Bland would probably appreciate a note informing him of this error so he can repair it in later editions. good question mr. amateur.

 

[Math Amateur]

Thanks so much to fresh_42, micromass and mathwonk for clarifying matters ... ...

The original question was posed by Steenis on the MHB site ...

Peter

 

[lavinia]

The counter example depends on the group being infinitely generated. What about the same question for a finitely generated R-module? For instance, what about a finite dimensional vector space?

- Also somewhat unrelated but perhaps noteworthy is that for finitely generated groups (not necessarily Z-modules) a split extension may not be a direct product.

 

[micromass]

The counter example depends on the group being infinitely generated. What about the same question for a finitely generated R-module? For instance, what about a finite dimensional vector space?

- Also somewhat unrelated but perhaps noteworthy is that for finitely generated groups (not necessarily Z-modules) a split extension may not be a direct product.

Yes, it will be true for finitely generated $R$-modules where $R$ is a Noetherian ring. In particular, it is true for all finite-dimensional vector spaces. Let me see if I can find a good reference.

 

[micromass]

Here is a short proof: http://mathoverflow.net/questions/1...ces-with-no-commutative-diagram-between-them/
For finite dimensional vector spaces the proof is much easier though, since in that case it's easy to see that any subspace has a direct summand.